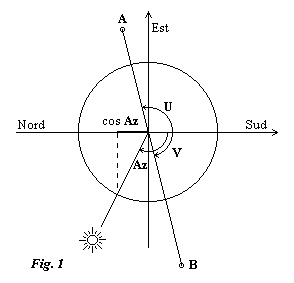
Définissons les conditions pour lesquelles on peut obtenir ce résultat. Il est d'abord nécessaire que l'ombre du premier gnomon A passe par le pied du second B, et inversement que l'ombre de B passe au pied de A. Exprimé d'une autre façon il faut que l'azimut du soleil puisse, au cours de la journée, être égal à l'angle de B vu de A et à l'angle de A vu de B. Reportons ces deux angles sur le cercle trigonométrique de la figure 1.

Pour qu'on ait Az = U et Az = V, le cosinus de Az doit donc changer de signe durant la journée et par conséquent s'annuler. Exprimons sa valeur en fonction de:
sin D = sin P.sin H - cos P.cos H.cos Az
sin D - sin P.sin H
d'où: cos Az = - ----------------------- (1)
cos P.cos H
cos Az = 0 <==> sin D = sin P. sin H
Etant donné que sin H est compris entre 0 et l'unité quand le soleil est au-dessus de l'horizon, cette relation implique que la déclinaison du soleil soit comprise entre 0 et la latitude du lieu, ces grandeurs étant signées.Considérons tout de suite le cas des zones polaires les jours où le soleil ne se couche pas. Cette situation se produit lorsque cos P < Abs (sin D) avec P du même signe que D, le soleil fait alors le tour de l'horizon et passe par tous les azimuts, donc obligatoirement par les prolongements de A et B quelles que soient leurs positions.
Pour les cas où le soleil se couche, définissons la direction R d'une droite L comme l'angle, compté dans le sens trigonométrique, que fait L par rapport à l'axe ouest-est. R(L) sera compris entre -90 et 90°. Pour chaque azimut du soleil on peut associer une droite L(Az) orientée en direction du soleil et ainsi une direction R(L(Az)) que nous désignerons par R(Az).
Pour que l'azimut du soleil passe par les prolongements de A et B il faut, lorsqu'on a vérifié la première condition, que la direction de la droite AB soit comprise entre les directions des azimuts du soleil à son lever et à son coucher. Le cosinus de ces azimuts est donné par la relation (1) pour H = 0 soit:
sin D
cos Azo = - -------
cos P
L'encadrement précédent peut se mettre sous la forme:
-Abs (cos Azo) < sin R(AB) < Abs(cos Azo) ou encore: Abs (sin R(AB)) < Abs (sin D/cos P)Ce sera la seconde et dernière condition.
Intéressons nous à présent à la courbe d'ombre de l'extrémité du gnomon A quand on vérifie la première condition et quand on se place dans le cas le plus restrictif, c'est à dire dans le cas où le soleil se couche. Cette courbe est une branche d'hyperbole qui, d'après la première condition, tourne sa concavité vers A et dont les asymptotes sont les droites associées aux azimuts Azo.
Remarquons que la direction d'une droite qui passe par deux points quelconques de cette branche est comprise entre les directions des asymptotes et de ce fait vérifie la seconde condition.
Pour que l'extrémité de l'ombre de A passe par le pied du gnomon B il faut que ce dernier soit situé sur la courbe d'ombre de A et que la direction AB respecte la seconde condition. De la même façon, pour que l'extrémité de l'ombre de B passe au pied de A il faut que sa courbe d'ombre passe par A. Dans ce cas les deux courbes ont toujours au moins un point commun situé entre A et B. Suivant la position de B sur la courbe d'ombre de A on peut avoir un ou deux points communs ainsi qu'on peut le voir sur la figure 2.
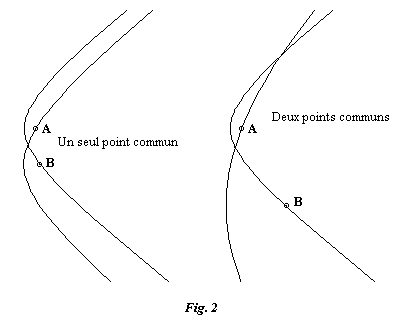
Si on place le troisième gnomon C sur un de ces points communs, les extrémités des ombres de A et B passeront au pied de C. A et C étant sur la courbe d'ombre de B, d'après la remarque faite plus haut la direction de AC vérifie la seconde condition et il sera toujours possible, en choisissant la bonne hauteur de C, que l'extrémité de son ombre passe au pied de A. B et C étant sur la courbe d'ombre de A, la direction de BC vérifie également la seconde condition et l'ombre de C se dirigera au cours de la journée en direction de B mais son extrémité passera-t-elle juste au pied de B ?
C'est ici que nous allons faire intervenir le théorème de Pascal qui s'énonce ainsi: soit a, b, c, d, e et f six points quelconques d'une conique, les points d'intersection des droites ab et de, bc et ef, cd et af sont alignés.
En conséquence, si les deux premiers points d'intersection sont rejetés à l'infini, ce qui signifie que la droite ab est parallèle à de et bc parallèle à ef, le troisième se trouvera aussi à l'infini et les droites cd et af seront également parallèles.
Soit hA, hB et hC la hauteur respective des gnomons A, B et C. Lorsque l'extrémité de l'ombre de B passe au pied de A, celle de A est dans le prolongement et son extrémité se trouve sur la courbe d'ombre de A au point E (figure 3) avec:
AB/EA = hB/hALorsque l'extrémité de l'ombre de B passe au pied de C, celle de A a son extrémité au point F avec:
CB/FA = hB/hALes angles ABC et EAF étant identiques, les triangles ABC et EAF sont donc semblables et EF est parallèle à AC.

Lorsque l'ombre de C est dirigée en direction de A, celle de A est dans le prolongement et son extrémité est située en G. Lorsque l'ombre de C est dirigée vers B, celle de A est dirigée à l'opposé de F et son extrémité se trouve en I.
Nous avons ainsi six points B, C, G, I, F et E situés sur la courbe d'ombre de A avec BC parallèle à IF et CG parallèle à FE, d'après ce que nous avons vu plus haut GI est donc parallèle à EB.
Les triangles AGI et CAB sont donc semblables car ils ont leurs cotés parallèles deux à deux. Ainsi, si la hauteur de C est telle que sa courbe d'ombre, qui est similaire à celle de A, passe au pied de A elle passera aussi par le pied de B.
Nous avons ainsi démontré qu'il existe une infinité de manières pour disposer trois gnomons sur une surface horizontale afin que l'extrémité de l'ombre de chaque gnomon passe au pied des deux autres au cours d'une même journée. Pour une date et une latitude qui vérifient la première condition, seul le choix de la hauteur d'un gnomon et la direction de l'alignement avec un second gnomon définit entièrement une ou deux configurations qui ont cette propriété. L'alignement doit vérifier la seconde condition et la hauteur du premier gnomon donnera la proportion de la configuration.
Bibliographie:
Retour à la page d'accueil -o- Reveno al la akcepta retpagho
Date de création: 21 Juin 99
Date de dernière mise à jour: 21 Février 2000