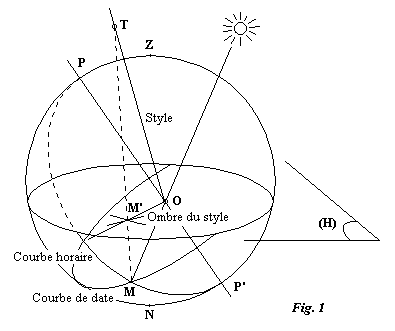
Le principe du tracé de tels cadrans repose sur l'utilisation d'une sphère fictive dont le diamètre PP' est parallèle à l'axe du monde. Imaginons que le plan horizontal (H) du cadran est transparent et qu'il coupe le diamètre PP' en un point O quelconque (fig. 1). L'ombre portée par O sur la sphère décrit en une journée une portion de cercle contenue dans un plan perpendiculaire à PP'. A la même heure vraie, l'ombre décrit au cours de l'année une portion d'un grand cercle qui passe par les points P et P'. Pour différentes heures et dates, les courbes ainsi parcourues forment un cadran sphérique fictif. La partie utile de ce cadran se situe sous le plan horizontal.

Soient Z le point le plus élevé de la sphère et N le point le plus bas. Prenons un point T situé sur ou sous le plan horizontal et tel que sa profondeur soit supérieure à celle de N si T est choisi sous le plan.
En utilisant la projection centrale de centre T, projetons la partie utile du cadran sphérique sur le plan horizontal et disposons un style porte-ombre rectiligne passant par O et T. Supposons que l'ombre du point O sur la sphère soit M à un instant donné et considérons M', projeté de M par la projection centrale. Le demi-plan d'ombre créé par le style contient M car le style passe par O. Il contient aussi M' car le prolongement de MM' passe par T et la demi-droite TM' est située dans le demi-plan d'ombre. De ce fait l'ombre du style sur le plan horizontal passe par le point M'.
Par extension, à une date et une heure données, l'ombre du style passera par l'intersection de la projection des courbes de date et d'heure correspondantes. La projection centrale de centre T du cadran sphérique fictif est donc un véritable cadran donnant l'heure par la position de l'ombre du style sur la courbe de la date de l'observation.
Les courbes du cadran sphérique étant des portions de cercle, leurs projections sont, dans le cas général, des portions d'ellipse ou d'hyperbole. Cependant si on choisit pour le lieu de T les points particuliers N ou Z, la projection centrale devient stéréographique et les courbes projetées deviennent des portions de cercle.
Il est intéressant de noter que l'intersection de la sphère avec le plan horizontal donne un cercle qui délimite la zone utile du cadran sphérique. Si T est choisi en Z, la projection de la zone utile est entièrement contenue dans le cercle; si T est choisi en N, la projection est entièrement à l'extérieur du cercle.
Lorsque le plan horizontal coupe la sphère en deux parties égales et que T est choisi en Z on obtient le cadran d'Oughtred avec son porte-ombre vertical.
Retour à la page d'accueil -o- Reveno al la akcepta retpagho
Date de création: 21 Février 99