Pour débuter cette nouvelle année, je vous propose l’analyse d’un petit document, aussi curieux que dépouillé, et qui s’avère d’une grande ingéniosité. Je n’ai, personnellement, jamais rencontré ailleurs le principe employé et je saurai gré au lecteur qui connaîtrait une autre publication à ce sujet de m’en informer, tout particulièrement si la démarche employée est purement géométrique.
C’est parmi les manuscrits de J.-H. Lambert conservés aux Archives municipales de Mulhouse que Jean_Marie_M a pu numériser cette demi-feuille d’environ 19x11 cm et qui, à première vue, semble représenter un quadrant de hauteur. Le soin apporté à la figure, tracée au compas et à la règle, suggère que Lambert a dû reporter sur cette fiche le résultat d’une réflexion qu’il a conduite par ailleurs.
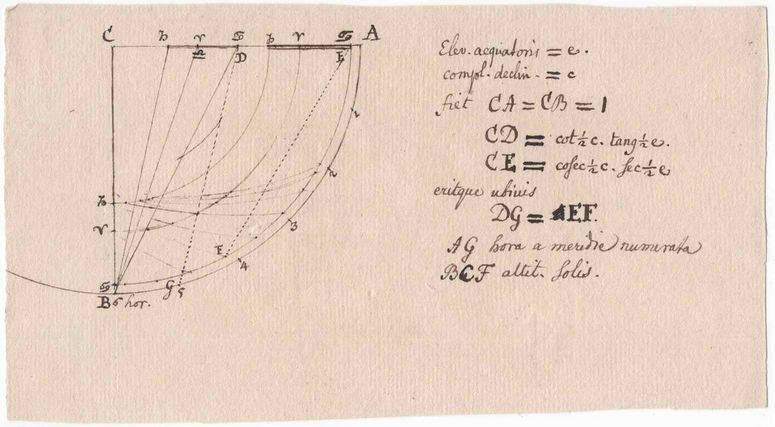
Les indications portées sur le côté sont particulièrement brèves et reprennent les notations habituelles de Lambert, qui se retrouvent notamment dans sa gnomonique :
- e = hauteur de l’équateur = 90° - ϕ
- c = complément de la déclinaison du Soleil = 90° - d
La relation de la distance CE semble toutefois incohérente car elle est constituée du produit de deux fonctions, cosecante (= 1/sinus) et secante (= 1/cosinus), qui sont toujours supérieures à l’unité. Essayons toutefois de la corriger en utilisant les grandeurs de la figure. Sur le segment des points D, l’angle CB
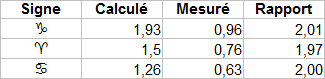
Ce qui permet de supposer que Lambert, qui avait la réputation d’être distrait, ait oublié un facteur ½ sur sa fiche. Nous verrons ci-dessous que c’est effectivement la bonne supposition.
La suite des indications semble donner une procédure graphique pour obtenir le tracés des courbes horaires. Il faut, dans un premier temps, graduer en heure la portion de cercle de rayon unité en utilisant l’angle horaire correspondant, soit 15° par heure, puis tracer des arcs de cercle à partir des points E pour différentes déclinaisons du Soleil, par exemple pour son entrée dans les différents signes du zodiaque. La courbe horaire de l’heure G (5 h sur la figure) est alors définie en reportant les distances entre le point G et les différents points D, prises par exemple avec un compas, sur les portions de cercle partant des points E correspondant aux mêmes déclinaisons que D, comme l’indique les deux segments en point-tillés de la figure pour l'entrée dans le Cancer. On obtient ainsi les différents points F de la courbe horaire.
En toute logique, le quadrant doit s’utiliser en suspendant, en C, un fil muni d’une perle P réglée sur le point E correspondant à la déclinaison du Soleil au jour de l’observation. Le quadrant est ensuite placé verticalement, le coin C dirigé vers le Soleil et la ligne CA dans l’alignement de ses rayons lumineux. L’angle ACP correspond alors au complément de la hauteur du Soleil et l’heure est indiquée par la perle sur le réseau des courbes horaires.
Voyons si la procédure du tracé, utilisée avec la relation de CE rétablie hypothétiquement, donne un quadrant rigoureux du point de vue mathématique. Posons, suivant l’habitude de Lambert :
- l’angle horaire ω = ACG
- le complément de la hauteur du Soleil k = 90° - h = ACF
- sx = sin ½x
- cx = cos ½x
Sur le quadrant, d’après la relation du triangle plan, nous avons :
DG² = 1 + CD² – 2.CD.cos ω
Soit avec la relation de CD proposée par Lambert :
DG² = 1 + cc².se²/sc²/ce² - 2.cc.se.cos ω/sc/ce
Par ailleurs, avec la relation supposée corrigée de CE :
EF = 2.sk.CE = sk/sc/ce
En rendant ces deux longueurs égales :
EF² = DG² ⇔ sk²/sc²/ce² = 1 + cc².se²/sc²/ce² - 2.cc.se.cos ω/sc/ce
⇔ sk² = sc².ce² + cc².se² – 2.sc.cc.se.ce.cos ω
⇔ 1 – 2.sk² = 1 – 2.sc².ce² – 2.cc².se² + 4.sc.cc.se.ce.cos ω
⇔ 1 – 2.sk² = 1 – 2.sc².(1 – se²) – 2.se².(1 – sc²) + 4.sc.cc.se.ce.cos ω
⇔ 1 – 2.sk² = 1 – 2.sc² – 2.se² + 4.se².sc² + 4.sc.cc.se.ce.cos ω
⇔ 1 – 2.sk² = (1 – 2.sc²).(1 – 2.se²) + 4.sc.cc.se.ce.cos ω
⇔ cos k = cos c.cos e + sin c.sin e.cos ω
On reconnaît la relation fondamentale de la trigonométrie sphérique appliquée au triangle de position Pôle-Zénith-Soleil, plus connue sous cette forme :
sin h = sin d.sin ϕ + cos d.cos ϕ.cos ω
et qui justifie la rigueur de la procédure et la validité de la relation de CE.
Ce qui est particulièrement astucieux avec ce quadrant, c’est qu’il est possible de le tracer entièrement sans aucun calcul de hauteur, calculs qui étaient particulièrement longs à conduire à l’époque de Lambert. Il est seulement nécessaire de connaître les lieux des points D et E qui peuvent être obtenus par les courbes suivantes :
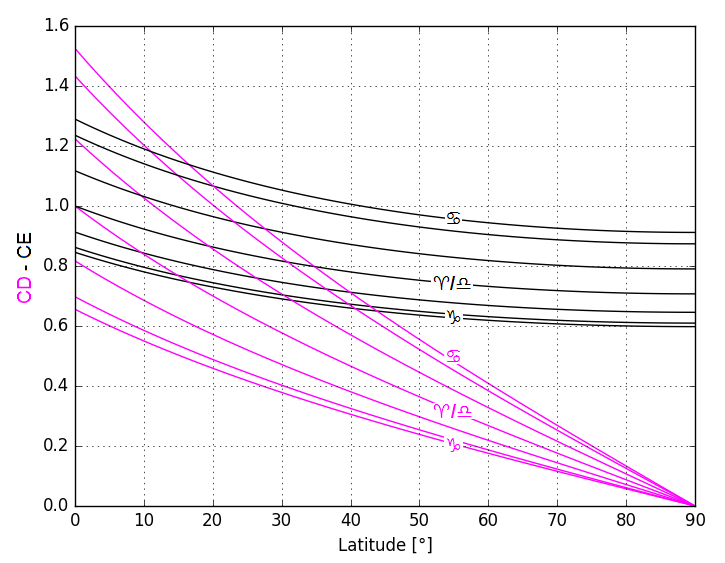
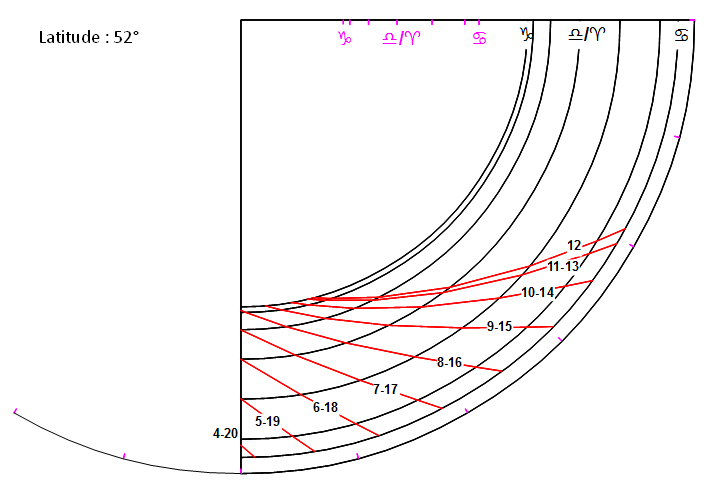
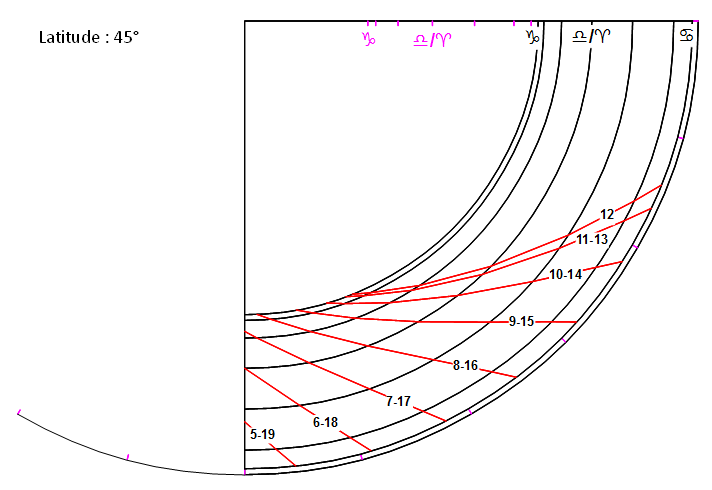
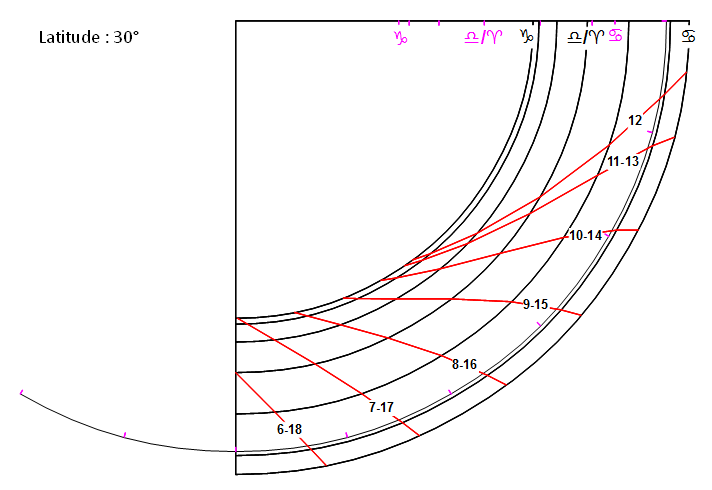
Ces courbes montrent aussi que la zone où sont tracées les lignes horaires reste dans des proportions parfaitement adaptées à ce type de quadrant, quelle que soit la latitude.
Enfin, pour illustrer cette analyse, voici le tracé de quadrants pour différentes latitudes. Les points de construction sont conservés en mauve pour permettre aux plus curieux de retrouver cette astucieuse propriété géométrique sur une impression, avec une règle graduée ou un compas :