Dans un premier temps, je la présenterai en l’adaptant légèrement pour qu’on puisse faire le lien avec le sujet « Recherche concernant une méthode graphique originale », je reprendrai notamment la notion de distance introduite par Gérard. Je donnerai ensuite la traduction du texte de Lambert. Enfin, dans un second message, j’apporterai des commentaires et éclaircissements sur la démonstration proposée.
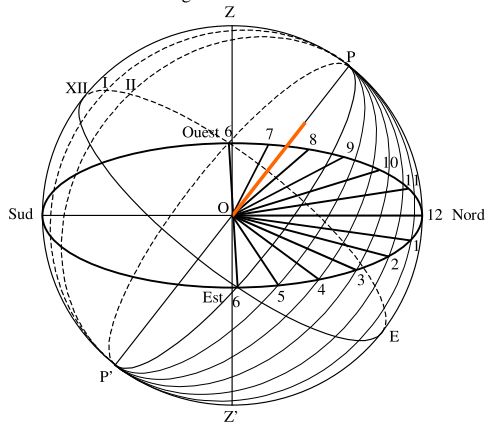
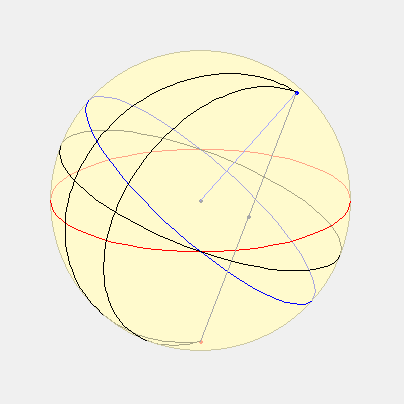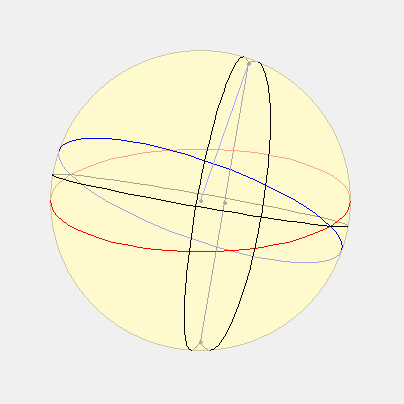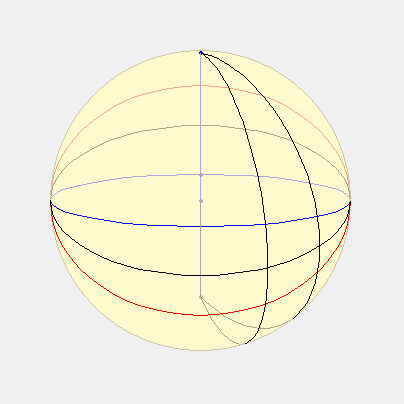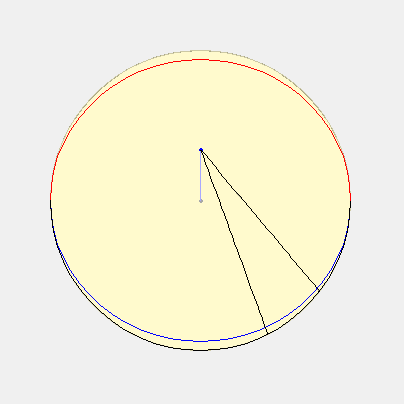
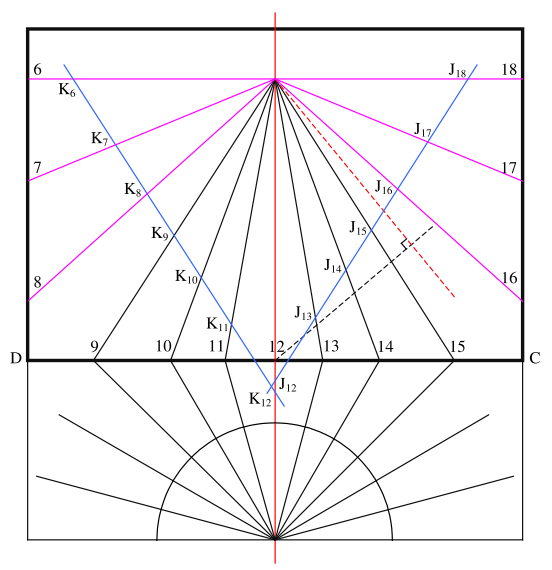
Voici donc la description adaptée : à partir du cercle de rayon R = GH, Lambert place le centre du cadran à la distance GE = R.cos(lat). Ensuite il gradue ce cercle non pas avec des intervalles égaux mais à l’aide d’un second cercle qui passe par le point H et qui a pour centre E. C’est ce dernier cercle qui est divisé en parties égales et, à partir du point P obtenu avec la bissectrice de l’angle GHE, les lignes tracées jusqu’aux divisions du second cercle permettent de graduer le premier. Les lignes horaires sont ensuite tracées comme dans la méthode de l’« oval pointu ».
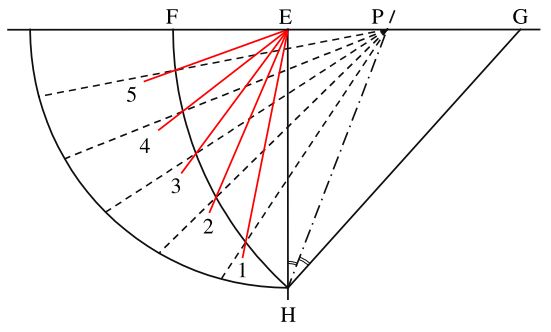
Voici maintenant comment J. H. Lambert présente cette méthode :
§ 43 Fig. XV
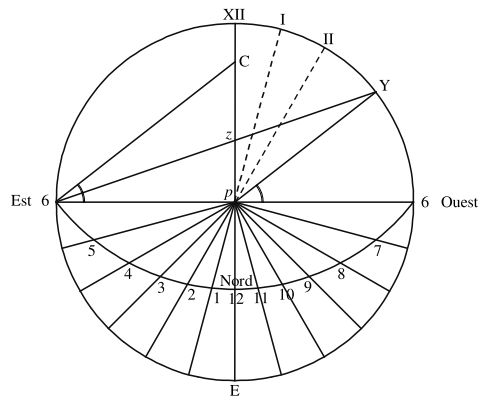
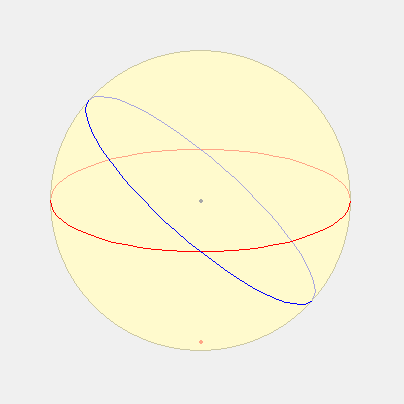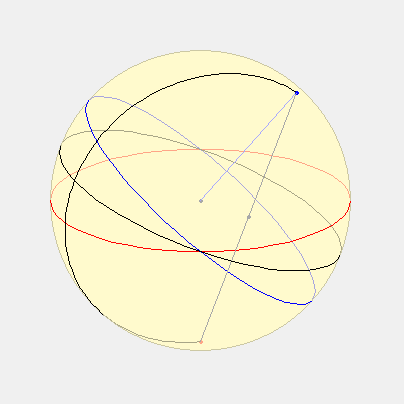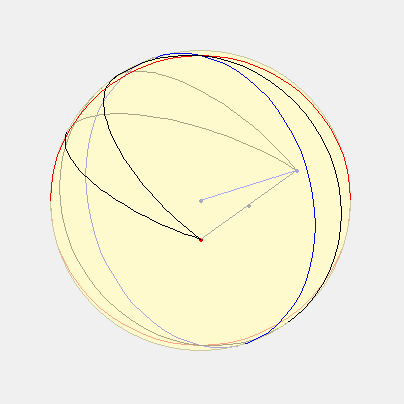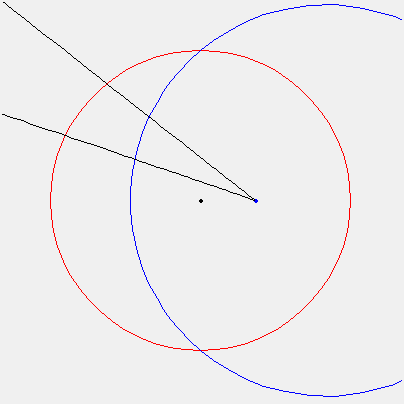
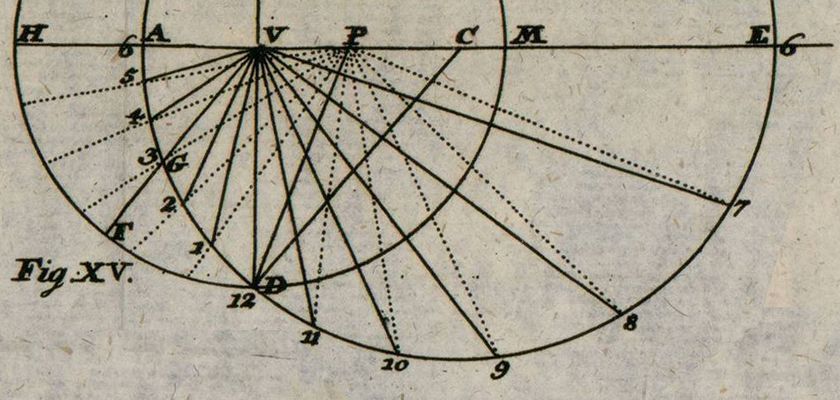
Que l’on trace donc le cercle HDM, ainsi qu’à l’intérieur les deux diamètres HM et VD, perpendiculairement. Partager ensuite le cercle HDM en 24 sections égales représentant les heures. Que l’on donne ensuite à VDC la hauteur de la ligne d’équateur, et à VDP la moitié de cette hauteur. Décrire ensuite le cercle ADE de centre C, passant par D. Tirer à partir de P des lignes aveugles vers chaque heure du cercle HDM, puis tirer à partir de V des lignes rejoignant les endroits où les lignes aveugles et le cercle ADE se coupent: ces lignes figureront les lignes des heures du cadran solaire horizontal pour la hauteur du pôle figurée par DCV.
§ 44
Le schéma est une projection de la sphère sur l’horizon. HDM est l’horizon, ADE l’équateur, P le pôle, V le zénith, VF un cercle vertical, DG l’arc des heures sur l’équateur, ou le temps à partir de midi transformé en degrés, GDF est la hauteur de l’équateur. Parce que le triangle DFG est rectangle en F, il en découle la formule suivante :
cos GDF = cot DG.tang DF
DF est donc l’arc des heures, ou DVF est l’angle des heures pour le cadran solaire horizontal. Les lignes aveugles PG n'ont d'autre fonction que celle de diviser la ligne d'équateur ADE en degrés selon les règles de la projection.