Pour utiliser cette méthode il est nécessaire de disposer d’une planchette dont la réalisation est décrite ci-dessous. Les choix proposés permettent de la réaliser à moindre coût tout en obtenant un dispositif fiable dont l’expérience a montré que les résultats obtenus était d’une précision plus qu’honorable et largement suffisants pour les besoins de la gnomonique.
Passons maintenant à la pratique :
Utiliser un morceau d’environ 40x40 cm d’une tablette blanche en particules de bois agglomérées généralement destinée à faire des étagères. La surface bien lisse permet de tracer précisément des traits au crayon qui peuvent ensuite être effacés à la gomme pour une nouvelle utilisation.
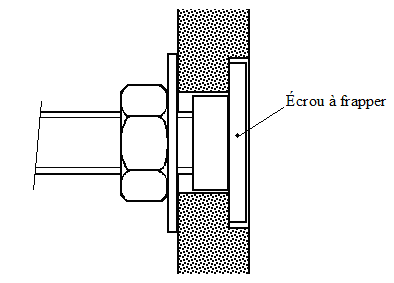
Vérifier que la planchette soit bien plane et choisir ou scier un bord bien rectiligne qui servira de référence. Pour le porte ombre, utiliser une tige filetée M8 ou M10 de 15 à 16 cm de longueur, trois écrous, une rondelle large, une petite plaque d’aluminium ou d’acier doux d’environ 1 mm d’épaisseur et un écrou à frapper, un truc qui ressemble à ça :

Percer un trou adapté à l’écrou à frapper au milieu de la planchette et à quelques centimètres du bord de référence. À l’aide d’un outil bien tranchant, pratiquez ensuite grossièrement un logement pour noyer entièrement l’écrou à frapper et mettre celui-ci en place.

À une extrémité de la tige filetée, visser un écrou sur quelques centimètres, enfiler ensuite la rondelle et visser la tige filetée dans l’écrou à frapper de façon que rien ne dépasse de l’autre côté de la planchette puis bloquer l’ensemble. La perpendicularité de la tige filetée par rapport à la planchette n’a pas d’importance, par contre elle doit être fixée bien rigidement.
Dans la petite plaque métallique qui sera découpée à environ 3x5 cm, percer deux trous. Le premier au diamètre de la tige filetée et le second d’un diamètre de 1 mm. Fraiser ensuite ce dernier, à l’aide d’une fraise ou d’un forêt, jusqu’à ce que le trou soit presque entièrement conique.

Fabriquer une équerre double avec une fiche bristol de 12,5x20 cm. Pour cela, à l’aide de l’extrémité d’un couteau pointu émoussé et utilisé comme un crayon, marquer une ligne au milieu de la fiche dans le sens de la largeur. Replier la fiche sur elle-même suivant cette marque et vérifier que les bords se superposent bien, ce qui signifie que l’équerre est correcte. Déplier alors la fiche jusqu’à obtenir un angle d’environ 90° et poser-la sur la planchette. Le pli est ainsi perpendiculaire à la surface de la planchette.
Le moment est venu de fixer la plaque sur la tige filetée à l’aide des deux écrous restants. Mettre la plaque en place, le plus petit diamètre du trou fraisé coté planchette, et régler sa hauteur de façon que l’équerre passe juste dessous sans frotter puis bloquer les écrous. Mesurer alors la largeur de la fiche, elle correspond à la hauteur du trou par rapport à la planchette.

Reporter ensuite la position du trou perpendiculairement à la planchette en utilisant le pli de la fiche bristol afin d’obtenir l’origine du système d’axes. Tracer celui-ci : l’axe des y parallèlement au bord de référence et positif vers la droite de la photo, l’axe des x perpendiculairement et positif du coté opposé au bord de référence (vers le bas de la photo).

La planchette est maintenant prête à être utilisée. Par une journée ensoleillée, quand la surface à mesurer est en plein soleil, il faut plaquer la planchette sur celle-ci et l’orienter à l’aide d’un niveau que l’on place sur le bord de référence, l’axe y est alors horizontal. Noter la position de la tache lumineuse correspondant au trou de la plaque par une petite croix au crayon en prenant soin de relever en même temps l’heure précise à quelques seconde près. Renouveler par sécurité cette opération deux à trois fois à quelques minutes d’intervalle, on peut constater à cette occasion que la tache de lumière se déplace assez rapidement, ce qui justifie de relever l’heure précisément.

À l’aide d’un réglet, mesurer ensuite la distances des croix aux axes x et y pour obtenir leurs coordonnées. Faire attention à utiliser le bon signe.
Avant d’effectuer les calculs, il faut maintenant déterminer la position géographique du lieu. Le plus simple est d’utiliser Google Maps : il suffit de cliquer sur la carte à l’endroit concerné, les coordonnés géographiques sont retournées dans la petite fenêtre qui apparaît en bas de l’écran sous la forme latitude, longitude. La longitude est positive à l’est du méridien de Greenwich, négative à l’ouest.
Il ne reste plus qu’à renseigner toutes les valeurs obtenues précédemment dans le formulaire proposé par Michel Lalos et suivre ses indications. Le formulaire se trouve ici :
http://michel.lalos.free.fr/cadrans_sol ... no-mur.php
Ajout :
Ou encore utiliser le formulaire suivant qui prend en compte automatiquement le changement d’heure été/hiver. Le cadran correspondant est dessiné à la fin du tableau.
Le tracé du cadran, comme l’ombre, peuvent se déplacer à la souris ou au doigt sur les tablettes et ordiphones. La molette ou deux doigts permettent d’agrandir et diminuer le tracé.
Bonne utilisation !