Le triangle AEC de J.-H. Lambert

[Yvon_M]

Dans le second tome de ses « Contributions à l’usage des mathématiques » publiées en 1770, Lambert utilise par deux fois, aux § 22 et 29 des « Ajouts à la gnomonique » , un triangle sphérique qu’il a nommé AEC pour introduire, après une projection stéréographique, deux instruments dont il est le découvreur. Le premier permet de déterminer l’azimut du Soleil et le second son angle horaire, ou l’heure vraie, en relevant, dans les deux cas, la hauteur du Soleil.



Dans l’opuscule sur l’analemme que j’ai publié en 2009 et qui se trouve ici :

Contenu réservé aux adhérents connectés.

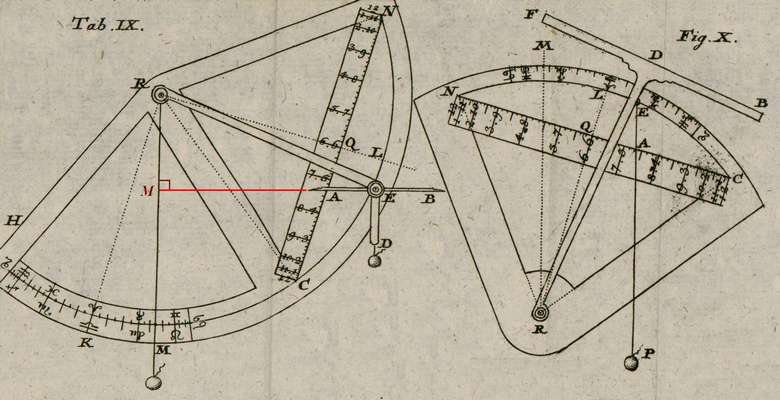
j’ai montré qu’on pouvait aussi retrouver le principe de ces instruments en utilisant la technique de l’analemme, soit sur le vertical du Soleil pour le premier instrument (p. 76), soit sur le méridien du Soleil pour le second (p. 26).

Dans cette contribution, je vous propose d’expliquer à l’aide de figures, insérées dans un diaporama et parfois animées, comment on peut faire le lien entre ces deux approches qui, sans surprise, sont équivalentes. Je commencerai dans ce premier message, suivant l’ordre de Lambert, par l’intrument qui fournit l’azimut et qui est représenté par cette très belle gravure :


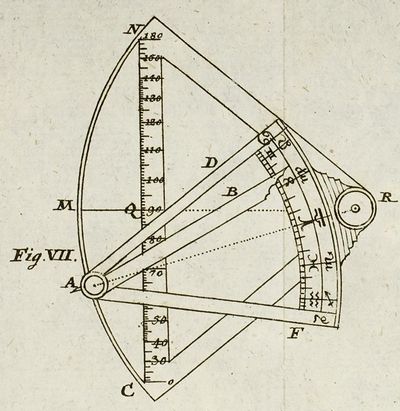
Crédit de numérisation : SUB, Göttinger Digitalisierungszentrum

La règle AB est mobile autour de l’axe A du secteur ADF qui, lui aussi, est mobile autour de l’axe R du secteur RNC. La règle AB doit être réglée suivant la déclinaison du Soleil et l’intrument est utilisé en maintenant la graduation CN verticale. En déplaçant le secteur ADF, la règle AB est alors dirigée vers le Soleil dont elle indique l’azimut par son intersection avec la graduation CN.

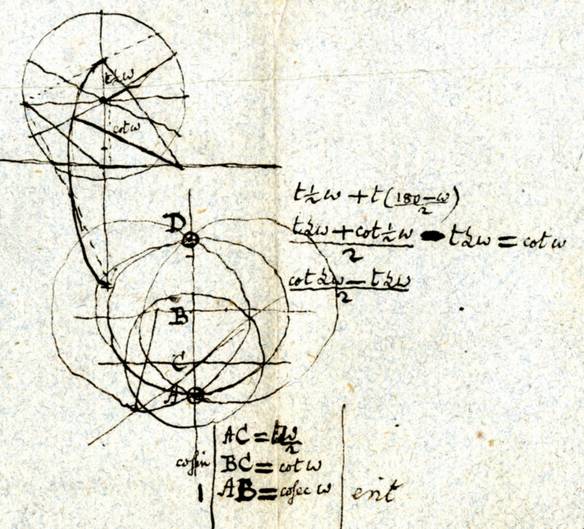
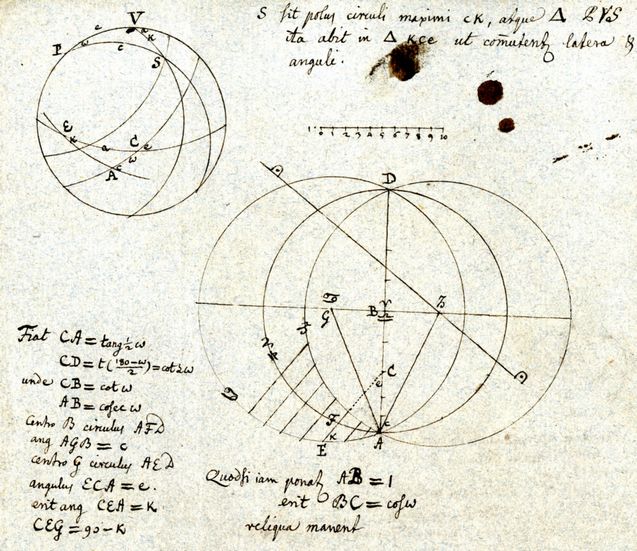
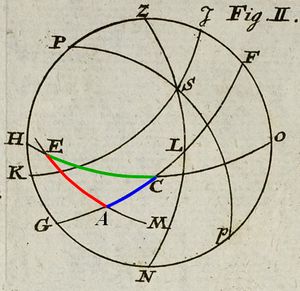
Revenons aux considérations géométriques utilisées pour définir ce cadran à partir du triangle AEC de la sphère. Lambert introduit la projection stéréographique qu’il va utiliser de cette manière : « Il s’agit maintenant de projeter le triangle AEC de telle sorte que l’œil soit sur la sphère à l’opposé du point E et que le tableau soit perpendiculaire à la ligne tirée de l’œil en E ».

Les termes « œil » et « tableau » sont empruntés à la perspective et correspondent respectivement aux centre et plan de projection de la géométrie projective. D’après les relations algébriques que Lambert donne ensuite, il apparaît que le plan de projection passe par le centre de la sphère. Comme le point E est sur l’horizon, le plan de projection est vertical. Enfin, comme E est sur l’«  horizon du Soleil » (le grand cercle dont le Soleil est le pôle), le plan de projection est précisément le vertical du Soleil, soit le même plan que celui utilisé avec la technique de l’analemme.

Dans le diaporama explicatif qui suit, j’ai utilisé un artifice pour obtenir la projection stéréographique de la sphère. Dans un premier temps, je l’ai orienté de façon que la figure elle-même soit dans le vertical du Soleil. La figure peut ainsi être considérée comme la projection de la sphère faite à partir d’un centre (l’œil) situé derrière la figure, à l’infini. En rapprochant progressivement le centre, la figure évolue. Quand il touche la sphère, la figure correspond alors à la projection stéréographique de celle-ci, ce qui donne au cercle de l’horizon la forme d’un cercle.

Je vous laisse naviguer dans le diaporama en cliquant sur les flèches qui se trouvent en bas des figures.



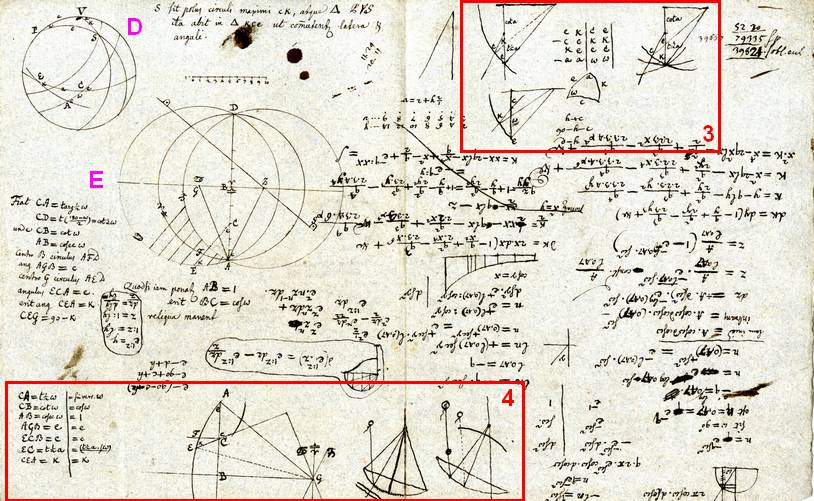
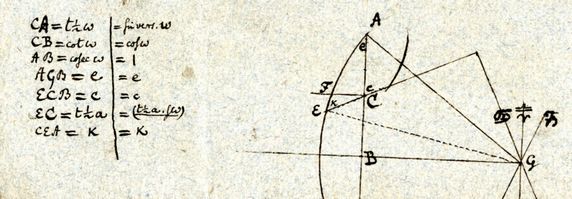
Voyons comment on peut confirmer rigoureusement que la projection de Lambert est équivalente à la construction par l’analemme. Ces deux projections sont superposées sur la partie droite de la figure suivante. Soit l’axe XX’ qui passe par les centres E et T des deux cercles (A) et (L). Par symétrie, cet axe passe aussi par le pied E’ du pôle Nord P. Considérons maintenant le plan (P) perpendiculaire à la figure et passant par l'axe XX’, il est rabattu sur la partie gauche de la figure et les traits en pointillé permettent de faire le lien entre les deux parties. Sur le rabattement, on retrouve le cercle (C) qui correspond à la trace de la sphère, UV est la trace de l’équateur qui est perpendiculaire à (P), le pôle Nord est sur le cercle en P et O est le centre de la projection stéréographique qui projette U en U’ et V en V’.

Les rayons IP et IO sont respectivement perpendiculaires aux diamètres UV et BD. De plus, d’après les propriétés du cercle, les cordes PB et PD ainsi que OU et OV sont perpendiculaires entre elles. Par ailleurs :

• IP ⊥ IU et IB ⊥ IO ⇒ les triangles IPB et IUO sont identiques et PB ⊥ UO
• PB ⊥ UO et PB ⊥ PD ⇒ UO ∥ PD
• PB ⊥ UO et VO ⊥ UO ⇒ VO ∥ PB
• UO ∥ PD, VO ∥ PB et U’V’ et BD sont sur la même droite ⇒ les triangles U’OV’ et DPB sont similaires et plus exactement homothétiques. Le centre d’homothétie est Y, soit la projection stéréographique de P, et le rapport d’homothétie est IO/HP. Un calcul trigonométrique montrera que IO/HP = 1/(sin Az.cos ϕ), Az étant l’azimut du Soleil et ϕ la latitude.

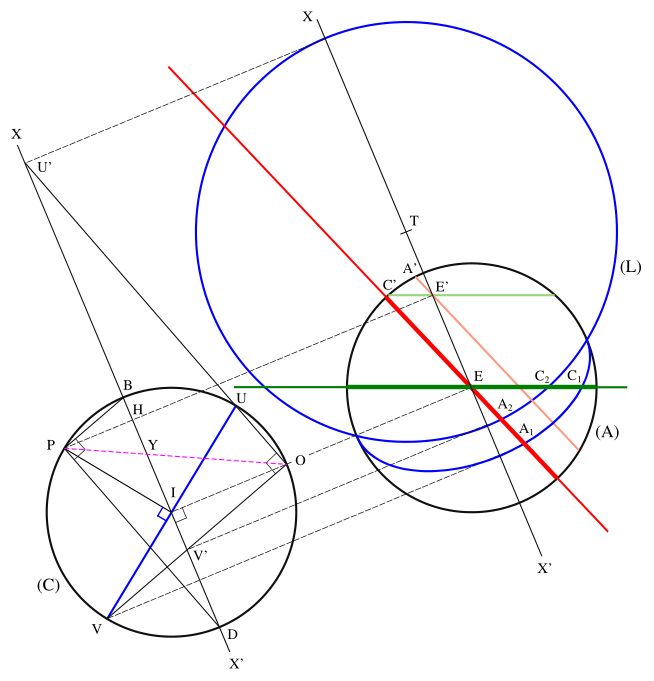
Les triangles U’OV’ et DPB permettent de définir entièrement la partie droite de la figure, ainsi on retrouve sur cette dernière la même homothétie entre les figures obtenues par projection stéréographique et la technique de l’analemme, ce qui confirme qu’elles sont parfaitement équivalentes.

Avec le recul, et sans vouloir en rien atténuer le grand génie de Lambert, il s’avère qu’il n’a pas utilisé la technique la plus simple et la plus régulière pour imaginer son cadran. Celui-ci se retrouve plus naturellement avec la projection orthographique de l’analemme. Il faut toutefois reconnaître que les cercles sur lesquels il s’est appuyé pour sa construction sont plus généralement utilisés que les cordes propres à l’analemme.

À plus tard pour la description du second instrument.

[Yvon_M]

Comme proposé, nous aborderons dans ce nouveau message le second instrument de hauteur que Lambert a introduit avec son triangle AEC et qui donne l’heure solaire. C’est sous deux versions différentes qu’il l’a proposé :


Crédit de numérisation : Numistral - Bibliothèques de l’Université de Strasbourg

La première version, à gauche, comporte deux masses pesantes. La masse de gauche permet de mettre l’instrument en position : ce dernier doit être dans le vertical du Soleil et le fil M doit indiquer sa déclinaison. On oriente ensuite le bras RE, mobile autours de l’axe R, pour que RE soit dans l’alignement du Soleil. La seconde masse pesante permet de placer la règle AB, mobile en rotation autour de l’axe E et solidaire de l’extension D, en position horizontale. La règle AB indique alors l’heure sur la graduation CN.

La seconde version de l’instrument, que Lambert présente comme une amélioration, ne comporte plus qu’une seule masse pesante mais son utilisation doit se faire en deux temps :

1. mise en position de l’instrument : le bras RE, mobile autours de l’axe R, doit être placé pour que E soit sur la déclinaison du Soleil. On oriente ensuite l’instrument dans le vertical du Soleil et de telle façon que le fil EP pende le long du bras RE.
2. relevé de la hauteur du Soleil : sans modifier la position de l’instrument, on tourne le bras RE pour que les pinnules F et B, dont la ligne de visée est perpendiculaire à RE, soient dans l’alignement du Soleil. Le fil EP indique alors l’heure sur la graduation CN.

Lambert introduit le principe de ce nouvel instrument par cette phase :
« […] je suis retourné au triangle ECA […]. Je l’ai projeté de manière à ce que l’œil soit sur la sphère à l’opposé de l’angle A et que le tableau soit perpendiculaire à la ligne qui sort de l’œil et qui passe par A. »

Comme le point A est sur l’équateur, le « tableau » est dans un méridien, c’est-à-dire un plan passant par l’axe des pôles. A étant aussi sur l’horizon du Soleil, le plan de projection est donc le méridien du Soleil.

Le diaporama qui suit permet de présenter les différentes figures et, comme dans le message précédent, de montrer le lien entre la projection de Lambert et celle de l’analemme.



La démonstration permettant de justifier l’homothétie entre les deux projections est similaire à celle du premier message. On peut également établir que le rapport d’homothétie est 1/(sin H.cos ϕ), H étant l’angle horaire du Soleil et ϕ la latitude.

Tel qu’ils ont été présentés ici, les instruments de hauteur pour mesurer l’azimut du Soleil et l’heure solaire ne sont utilisables que pour une seule latitude, celle qui se retrouve dans l’angle QRC ou QRN. Pour palier à cette limitation, Lambert proposa une façon de rendre ces instruments universels, en déplaçant la graduation CN en fonction de la latitude.



Dans ses Ajouts à la gnomonique, c’est sur cette universalisation que Lambert termine l’exploitation de son triangle AEC. Il reste toutefois un « tableau » sur lequel on peut projeter ce triangle pour obtenir deux droites et un cercle : celui qui est perpendiculaire au diamètre aboutissant au troisième point C, intersection de l’horizon et de l’équateur. Le plan correspondant est le méridien du lieu.

Bien que Lambert ne l’évoque pas dans ses Ajouts à la gnomonique, nous verrons dans le prochain message qu’il a probablement initier la démarche qui l’a conduit à imaginer les instruments ci-dessus en utilisant précisément la projection stéréographique du triangle AEC sur le méridien du lieu.

[Yvon_M]

Les archives municipales de Muhouse conservent des notes autographes de Lambert où se trouvent des annotations, figures, croquis et relations algébriques qui sont, en partie, à l’origine de la matière des Ajouts à la gnomonique. Une partie des ces notes est numérisée et consultable sur Internet, ici :
https://omeka.numistral.fr/s/numistral/item/84592
(nous en avons déjà parlé sur ce forum dans ce sujet : viewtopic.php?t=175)

C’est à partir de ces numérisations que nous essaierons de retrouver le fil de réflexion qui a conduit Lambert au triangle AEC et, par suite, aux instruments des messages précédents. Certaines notes, dont celles qui nous intéressent, sont un véritable fouillis et comportent souvent plusieurs sujets sur une même page, ce qui laisse penser que Lambert était bien dans une démarche de recherche quand il noircissait ces pages : la seule logique semble être l’utilisation systématique de toute la surface disponible. C’est donc par prélèvement que nous retiendrons les croquis ou figures qui correspondent visiblement à notre propos.

Parmi les 7 numérisations présentées et proposées en téléchargement (la 8e correspond à la zone centrale de la première numérisation) nous retiendrons celles numérotées 2 et 5 reproduites ci-dessous.

Sur la numérisation n°5, la seule figure qui semble exécutée avec soin est la projection orthographique de la sphère sur le plan du méridien, en A. Lambert s’en est visiblement servi pour tracer par une méthode graphique, via le demi-cercle B gradué en dizaines de degrés, le cadran de hauteur C.


Crédit de numérisation : Numistral - Archives de Mulhouse

Lambert était peut-être alors imprégné des problématiques propres à ces cadrans quand il a rajouté les croquis encadrés sur lesquels nous porterons notre attention. Voici l’encadré 1, débarrassé de tout ce qui semble ne pas être concerné :



Le diaporama suivant montre comment on peut retrouver la figure principale de cet encadré et comment on peut supposer qu’elle a conduit à l’encadré 2.



Sur la numérisation n°2 on retrouve, tracées avec grand soin, en E la figure principale de l’encadré 1 et, en D, la sphère de l’encadré 2, signe que Lambert y a vu un résultat digne d’intérêt.



Regardons de plus près ces figures qui sont accompagnées des relations donnant les différentes longueurs de la projection.



La sphère sera reproduite pratiquement à l’identique dans les Ajouts à la gnomonique. Quant à la projection, elle est ici plus complète que sur la numérisation n°5 et elle laisse apparaître plus distinctement les lignes du capucin avec notamment ses pinnules sur la droite perpendiculaire à CE.

Notons enfin que l’on retrouve sur cette projection, aux mêmes endroits, les mêmes lettres repères que sur la figure principale de l’encadré 1 : A, B, C et D. La prochaine sera E qui servira pour le troisième angle du triangle sphérique AEC dont nous avons maintenant, en quelque sorte, l’étymologie.

C’est ensuite que Lambert semble avoir envisagé d’utiliser d’autres « tableaux » pour la projection stéréographique. Il n’a toutefois pas fait appel à la méthode que nous avons utilisée plus haut, dans les premiers messages, mais il a procédé par permutation des angles du triangle PVS de la sphère D (c.-à-d. le triangle de position) comme on peut le voir dans l’encadré 3 reproduit ci-dessous.



Le triangle y est reproduit avec ses différents angles qui sont aussi listés dans la troisième colonne du tableau central. Dans les 3 colonnes attenantes, Lambert a listé les 3 permutations possibles comprenant soit l'angle a soit l'angle ω et qui donnent les 3 croquis associés :

• F : c’est le croquis qui donnera l’instrument de mesure d’azimut du premier message. Malheureusement aucune note conservée aux archives de de Mulhouse ne comporte les traces des développements que Lambert dû probablement faire sur cette configuration.
• G : le plan de projection est, ici encore, le méridien et l’angle recherché est l’azimut. Comme signalé en conclusion de De l’Analemme aux cadrans de hauteur, cette configuration n’aboutira à aucune réalisation pratique.
• H : ce croquis sera à l’origine de la première version de l’instrument donnant l’heure et présenté dans le second message. Nous retrouvons la structure de cet instrument, qui n’a visiblement pas encore trouvé sa forme définitive, dans la partie gauche de l’encadré 4 reproduite ci-dessous avec la quantification des différentes longueurs.

C’est en retournant l’encadré qu’on peut associer plus facilement les différentes parties de l’instrument à sa figure théorique.



Et on a même la surprise de retrouver sur la partie gauche (ce qui était à droite avant retournement) le croquis de la seconde version améliorée de cet instrument (au centre) et même, complètement à gauche, une troisième version que Lambert a visiblement abandonnée. Cette dernière version utilise, comme la première, deux masses pesantes. Celle de gauche est fixée au bâti et permet d’incliner l’instrument de la déclinaison du Soleil suivant une échelle que Lambert a symbolisée par un arc de cercle près de la masse pesante. La seconde masse pesante est celle que Lambert a conservée dans sa version améliorée, elle est fixée au bras articulé et indique l’heure sur la corde de l’arc de cercle supérieur.

Ma contribution se termine ici. J’espère que ce voyage dans les spéculations et les productions du grand génie qu’était Jean-Henri Lambert vous a intéressé. Pour ma part, j’étais loin d’imaginer que ces quelques notes pouvaient me fournir autant de clefs pour retracer une toute petite partie du parcours, qui reste toutefois hypothétique, de cet auteur particulièrement prolifique.

[sebB]

Merci Yvon pour cette brillante étude géométrique du Travail de J-H Lambert.
Merci de nous la faire partager.
seb

[Stéphane_L]

Passionnant, avec des diaporamas particulièrement éclairants. Merci, Yvon.

[Jean-Marie_M]

Un immense merci, Yvon, pour ce remarquable décryptage. A la façon d'un diamantaire de talent, vous avez su faire jaillir de la pierre brute mille éclats de connaissance. Ce trésor du mois qui, lors de sa mise au jour par l'archiviste, était un précieux mais obscur grimoire, est ainsi magnifié par votre expertise. En nous ouvrant la route de la lumière vous nous donnez à voir et comprendre, au fil de ses réflexions et des vôtres, le travail de l'admirable Lambert.