Pour avoir une idée plus précise de la problématique on peut consulter le document :
http://assprouen.free.fr/dossiers/volve ... lv-Cal.pdf
dont j’ai extrait, pour illustration, la figure suivante de Pierre Causeret. Elle a l'avantage d’être conçue pour notre époque moderne.
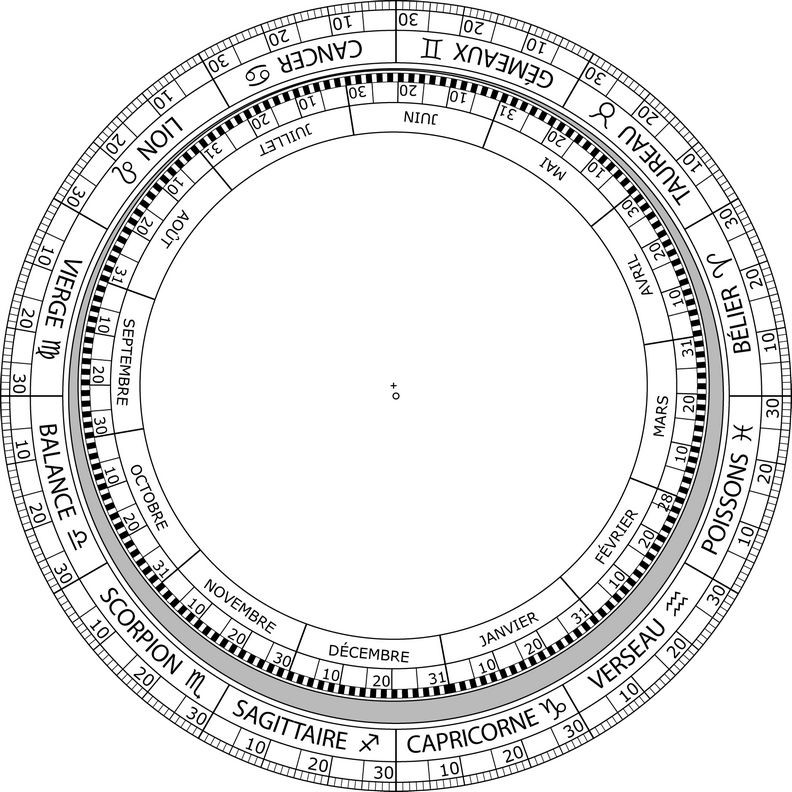
Les jours du calendrier ordinaire sont répartis uniformément sur le cercle excentré qui est ici central, mais qui pourrait aussi, en principe, être externe. Son centre est représenté par une croix. Chaque jour correspond à un angle constant de 360/365° (il n’y a pas de 29 février).
Les signes du zodiaque sont sur le cercle extérieur dont le centre est représenté par un petit rond. Il sont aussi répartis uniformément : chaque signe occupe 30° et chaque degré d’un signe fait, comme son nom l’indique, un angle de 1°, exactement.
Pour passer d’un calendrier à l’autre, il suffit de tirer un rayon à partir du petit rond (ou tirer un fil fixé sur ce repère) et passant par la date choisie d’un calendrier pour lire la date correspondante sur l’autre calendrier, là où passe le rayon.
Du point de vue de la mécanique céleste, ce graphique permet de résoudre le problème de Kepler pour l’orbite elliptique de la Terre qui est caractérisée par l’excentricité e = 0,0167. En principe, ce que nous confirmerons, le rapport entre la distance d séparant le centre des deux cercles et le rayon R du cercle excentré est d/R = 2.e
On comprendra aussi facilement que le diamètre commun aux deux cercles, qui passe par la croix et le petit cercle, passe aussi :
- du côté de la croix par la date de l’aphélie, vers le 5 juillet, quand la Terre évolue le plus lentement autour du Soleil
- à l’opposé, du côté du petit cercle, par le date du périhélie quand la vitesse de la Terre autour du Soleil est maximale, vers le 4 janvier
- anomalie moyenne M pour initier les calculs, elle est proportionnelle au temps et augmente donc de 360° en une période de révolution. Dans notre cas c’est l’angle, vu de la croix, entre une date du calendrier ordinaire et le 4 janvier.
- anomalie excentrique E qui est un angle intermédiaire mais que nous n’utiliserons pas ici
- anomalie vraie v qui est l’angle cherché
v \(=M+2\cdot e\cdot \sin (M)+\frac{5}{4}\cdot e^2\cdot\sin (2\cdot M)\)
Nous la comparerons à l’angle du calendrier ordinaire vue du petit rond, c’est-à-dire :
v’ \(=\arctan(\frac{R\cdot\sin (M)}{R\cdot\cos (M)-d})=\arctan(\frac{\sin (M)}{\cos (M)-d/R})\) à 180° près
On pourrait mathématiquement effectuer le développement de v’ pour établir la différence avec v mais, comme le but est d’obtenir l’ordre de grandeur de l’erreur, nous utiliserons plus simplement les résultats d’un tableur. La figure des deux cercles étant symétrique par rapport à leur diamètre commun, il suffit de faire une comparaison pour M variant de 0 à 180°. Enfin, un calcul tous les 5° donnera un tableau de 36 lignes, nombre suffisant pour évaluer l’évolution de l’erreur et sa valeur maximale.
Voici les résultats obtenus :
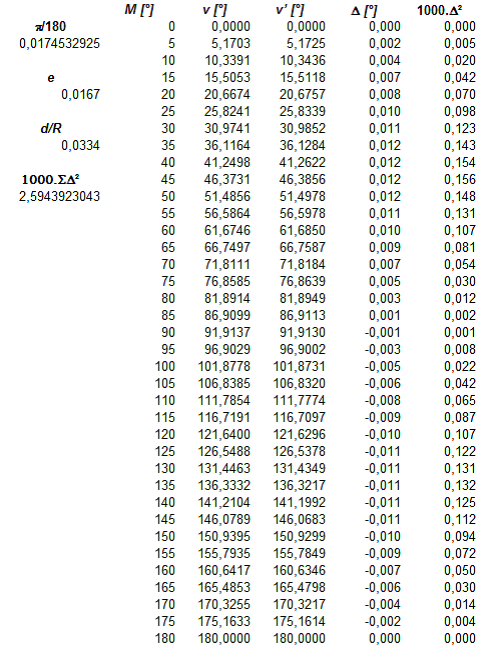
On peut constater, dans la colonne \(\Delta\) = v’ – v, que l’erreur maximale est de l’ordre du centième de degré, soit inférieur à la minute d’arc. C’est plus que suffisant dans le cadre d’une utilisation graphique qui, par ailleurs, ne permet pas de se positionner précisément sur le calendrier ordinaire à cause du décalage progressif dans le cycle de 4 ans des années bissextiles.
La dernière colonne correspond au carré des différences \(\Delta\) multiplié par la constante arbitraire 1000 afin que la valeur obtenue soit plus facile à lire. La somme de ces valeurs est indiquée à gauche et elle permet de vérifier que le rapport d/R est optimum. On peut, en effet, faire varier celui-ci de façon à obtenir une somme minimale, ce qui est un critère de la bonne approximation de l’anomalie vraie. La valeur obtenue est d/R = 0,0033393, légèrement plus faible du double de l’excentricité e mais on peut constater que les valeurs \(\Delta\) sont pratiquement inchangées.
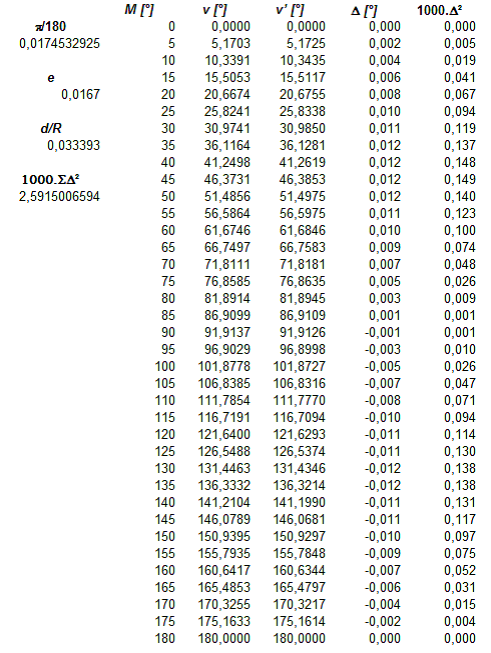
En conclusion, on peut confirmer que l’erreur de principe de ce graphique à cercle excentré de d/R = 0,0334 est négligeable en regard des erreurs inhérentes à son utilisation et justifie pleinement sa raison d’être.
Le fichier tableur utilisé peut être téléchargé en cliquant sur ce lien.