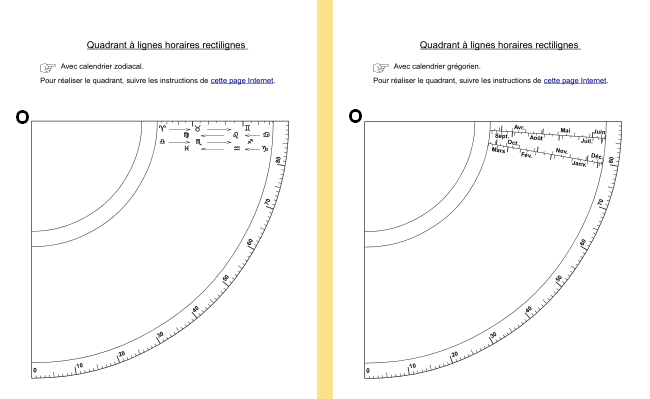
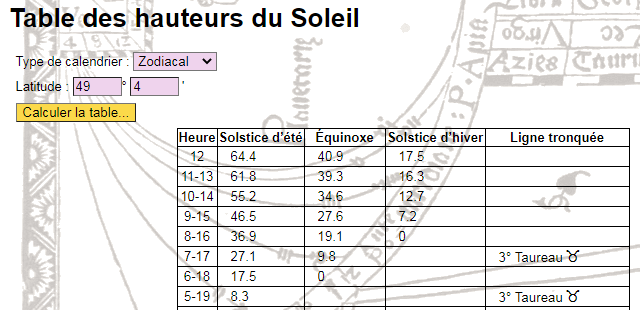
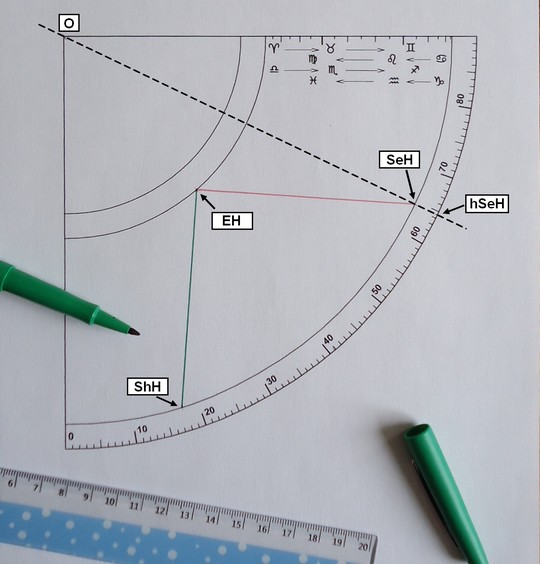
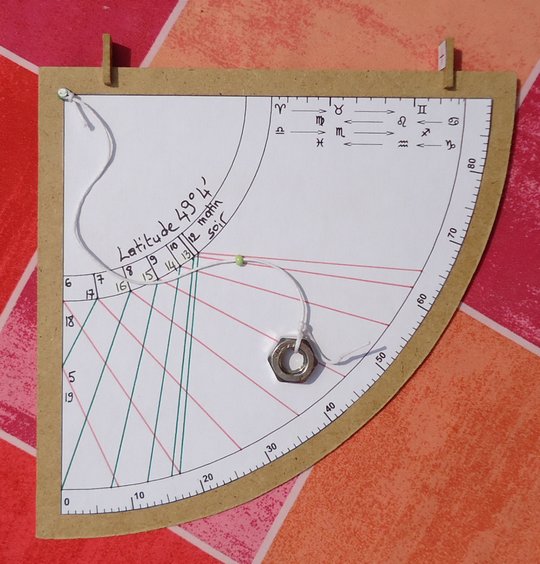
Sur la figure suivante on peut voir comment se présente le quadrant, il se compose d’une table en quart de disque (d’où l’orthographe un peu particulière de son nom) surmontée de deux pinnules et disposant d’un fil lesté suspendu au centre O.
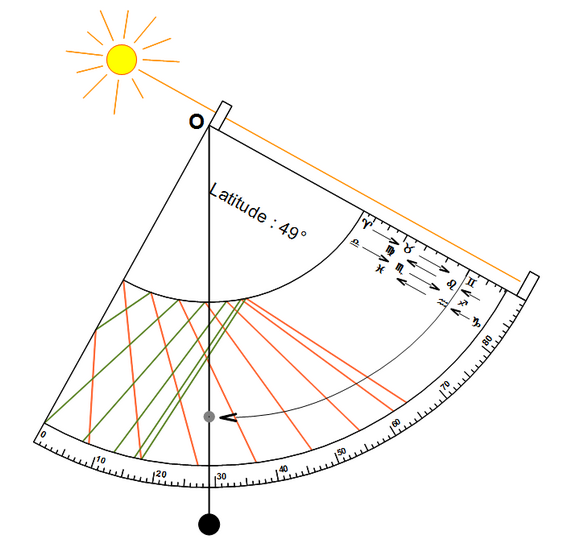
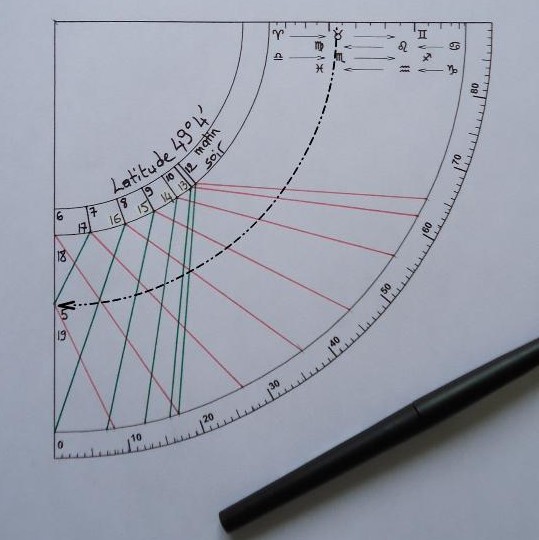
Une perle coulissante sur le fil doit être réglée à la date d’utilisation. Un calendrier est gradué sur le quadrant pour cet usage, il est replié trois fois sur lui-même avec un pli par saison : les équinoxes sont au plus près du centre O et les solstices au plus loin. Sur la figure la perle a été réglée à l’entrée des Gémeaux, soit le 21 mai. Le quadrant est ensuite présenté au Soleil en alignant les pinnules dans sa direction et en maintenant le plan du quadrant vertical. La perle indique alors l’heure qu’il faut lire entre :
- les lignes oranges du début du printemps à la fin de l’été,
- les lignes vertes du début de l’automne à la fin de l’hiver.
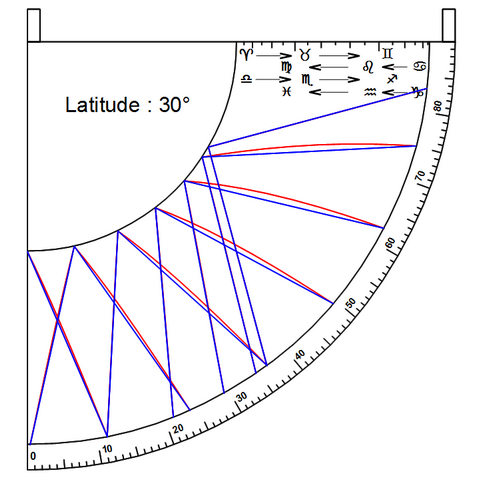
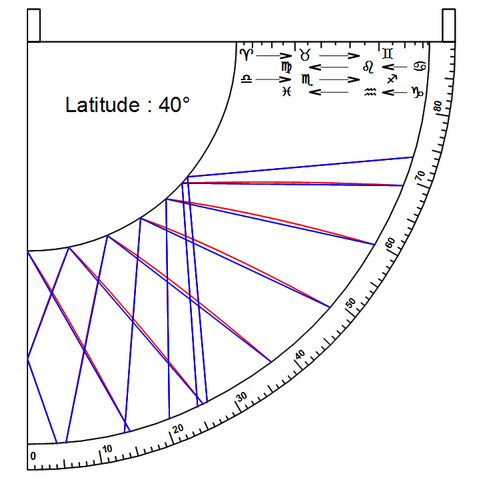
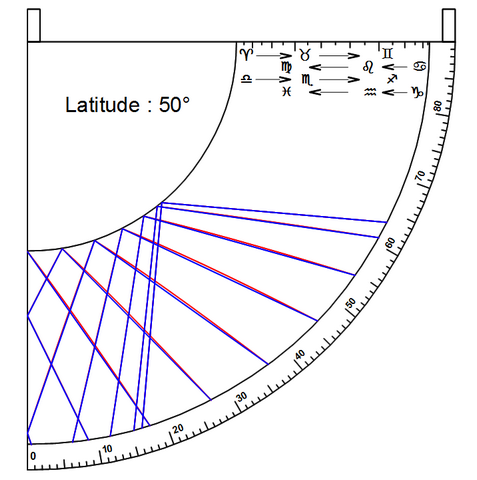
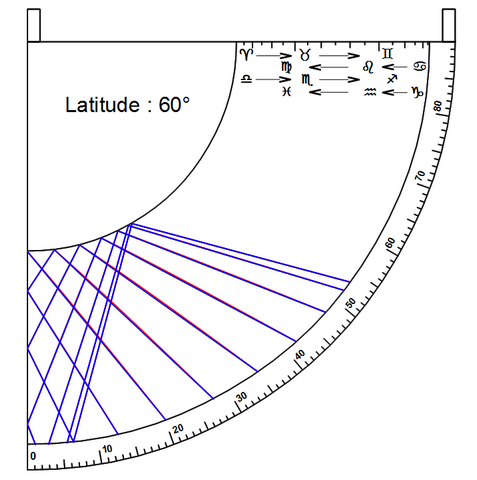
L’approximation du tracé rectiligne des lignes horaires est directement reliée à celle faite pour l’anneau à trous fixes présenté sur ce forum. Comme pour l’anneau, l’approximation est d’autant meilleure que la latitude est élevée. Les graphiques suivants où sont tracés pour chaque heure, en rouge, les véritables courbes horaires et, en bleu, les droites approximatives donnent une bonne idée de la précision que l’on pourra en attendre. Il est assez remarquable de constater que la superposition de la courbe et de la droite est presque parfaite pour l’automne et l’hiver, même dans le cas de faibles latitudes.
On trouve les premières descriptions imprimées de ce quadrant dans l’ouvrage de Stöffler paru en 1513, Elucidatio fabricae ususque astrolabii (1). Bien que cet ouvrage ait eu de nombreuses rééditions et une traduction en français (2), le quadrant ne semble pas avoir eu un grand succès et seuls quelques rares exemplaires sont conservés dans les musées.
La bibliothèque d’état de Bavière, à Munich, conserve un recueil de planches attribuées au graveur G. Hartmann (3) parmi lesquelles on trouve deux représentations de ce quadrant – merci Eric_M pour cette référence –. La première semble datée de 1519 (il faut chercher les chiffres autour de la fleur de l’autre quadrant de la gravure) et la seconde est de 1561 (là encore la date n’est pas mise en évidence, il faut la chercher dans le coin du quadrant, tout en bas de la gravure). Le système de graduation des lignes horaires d’Hartmann est plus simple que celui proposé par Stöffler, il est situé presque entièrement près du quart de cercle des équinoxes, ce que Stöffler avait appelé le limbe mineur.
Dans Protomathesis paru en 1532 (4), O. Fine fait une description de ce quadrant avec un réglage de la perle différent. À l’image du quadrant ancien décrit sur ce forum, le calendrier est disposé le sur bord circulaire. Il n’y a dans ce cas qu’un seul repliement mais la position même du calendrier dépend directement de la latitude. Quand le fil est tendu sur la date d’utilisation, la perle doit se régler sur ligne horaire de midi.
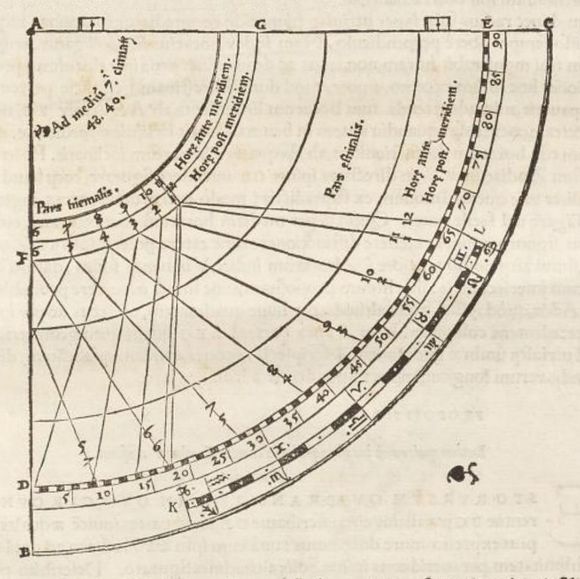
Dans son Cours de mathématiques de 1693 (5), en annonçant « On peut encore représenter les heures par des lignes droites, sans que l’erreur puisse être aussi beaucoup considérable […] », Ozanam décrit les étapes nécessaires pour tracer ce quadrant et il reportera l’année suivante un texte similaire dans ses Récréations mathématiques (6). C’est à l’un de ces deux ouvrages très pédagogiques que je vous renvoie pour toutes les précisions nécessaires concernant la géométrie de ce quadrant.
Plus récemment M. Sauzay, sur son blog Astro-Alps, a proposé une description de différents quadrants de hauteur indiquant les heures solaires (7) et il termine par celui qui est présenté ici en soulignant son ingéniosité.
Enfin dans Cadran-Info, le bulletin de la commission des cadrans solaires, une étude très détaillée de ce quadrant a été publiée par D. Savoie (8) – que je remercie ici d’avoir accepté de la partager –. À ma connaissance, c’est la seule publication qui aborde les relations algébriques permettant de quantifier l’erreur de mesure introduite par le principe du cadran.
À bientôt pour le passage à la pratique.
Bibliographie :
1 ^ - J. Stöffler : Elucidatio fabricae ususque astrolabii, fol. LXVIr. Oppenheim, 1513
2 ^ - J.-P. de Mesmes : Traité de la composition et fabrique de l’astrolabe, p. 184. Paris, 1560
3 ^ - G. Hartmann : Recueil de planches, fol. 3r, fol. 39v
4 ^ - O. Fine : Protomathesis. De solaribus horologiis et quadrantibus, fol. 190r. Paris, 1532.
5 ^ - J. Ozanam : Cours de mathématiques, tome V, p. 141. Paris, 1693
6 ^ - J. Ozanam : Récréations mathématiques, tome I, p. 281. Paris, 1694.
7 ^ - M. Sauzay : Astro-Alps. Les quadrants d’heures classiques (i.e. égales). 2014.
8 ^ - D. Savoie : Cadran-Info n° 41. Cadran solaire portable à double limbe. 2020.