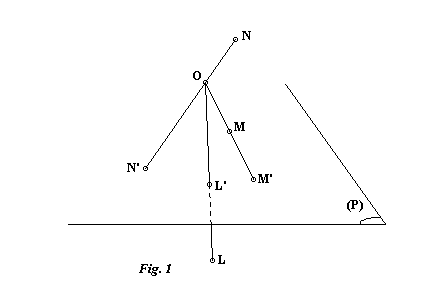
We begin by briefly recalling what the central projection from center O onto a plane P is. It projects any point M onto a corresponding point M' in the plane P such that O, M and M' are collinear (Fig. 1).

All the points in space thus have a projection on P (for example, L and N in the figure), except the points contained in the plane parallel to P and containing O. Note that this plane marks the boundary between the set of points, such as L and M, whose projections are on the same side of O on the projection line and the set whose projection points are situated on the other side of O, such as N in the figure.
Consider Figure 2 where we see the point A of the axis PP' of an auxiliary armillary dial casting the shadow M onto the equatorial circle (E) with center C. The angle AMC is thus equal to the declination of the sun. Let us place a straight vertical shadow-casting style passing through A and an arbitrary point O which will be taken as the center of the projection. In using the central projection, we project the point M onto the dial plane (P) chosen so as to obtain the point M' on the same side of O (as M) on the projection line. The half-plane of shadow created by the style contains M because the style passes through A. Since it also passes through O, the line segment OM, which contains M' (which is not the case if M' is situated on the other side of O), also belongs to the half-plane of shadow. Consequently, the style's shadow on the dial passes through M'. Note that this remains true if the point O is situated behind the observable face of the dial.
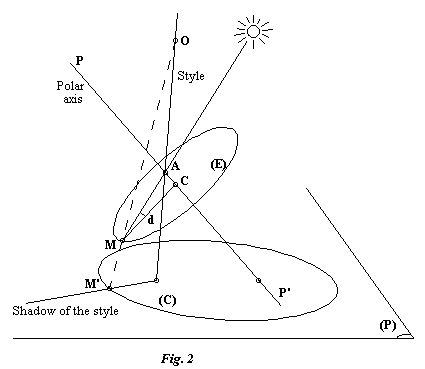
The circle (E) is graduated as usual (15°/hr) so that the hour can be read by the position of the point M. If we project from O the entire circle (E), graduation by graduation, we obtain a graduated curve (C) belonging to the family of conics. The hour can thus be read by the intersection of the style's shadow with the curve (C). To conserve this property throughout the year, it suffices to have the style always pass through the center O and the point A which moves on the axis of the auxiliary dial through the course of the seasons. It is therefore necessary to move the style in rotation around the point O. As a practical matter, we can locate the position of the style by the proper placement of its foot on the dial for certain dates. These date marks correspond to the central projection through O of the positions of the points A on the chosen dates.
Now we determine the type of conic that we obtain as a function of the positions of the center O and of the circle (E) with respect to the plane of the dial. For that we will refer to the height of a point as the distance of the point to its orthogonal projection on the dial while choosing, for example, the positive heights for points situated in front of the dial and negative for points situated behind. All the points of the circle (E) thus have heights included between two values which we will call hm and hM. As a function of the height hO of the point O, we distinguish the three following cases:
Bibliography:
Return to the home page -o- Reveno al la akcepta retpagho
Date written: 31 August 97
Date translated: 4 February 98