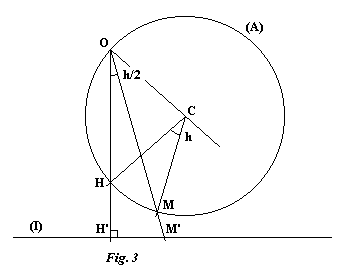

Let O be the chosen center of projection and (I) the line of intersection of the equatorial plane and the surface of the sundial. For a horizontal sundial this must be an east-west line. Let H be the hour mark on the auxiliary circle which projects to H' such that OH' is perpendicular to (I). Lastly let M be an hour mark distant from H by the angle MCH = h. From the properties of a circle we know that the angle HOM = h/2 and the point M', the projection of M, is at a distance from H' of M'H' = OH'.tan (h/2). As for the style, it must pass through O and through the active point of the gnomon of the auxiliary sundial. The equivalent of the sub-style in the equatorial plane is thus the line OC. Note that the angle between the style and this sub-style is equal to the declination of the sun for this date when the equation of time is zero.
For a value E of the equation of time we turn the auxiliary circle by this value, and we can imagine that the point H is fixed, and that we have moved the center C along the perpendicular bisector of OH (see figure 4).
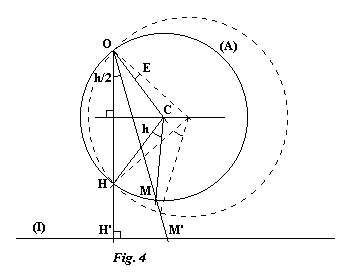
The radius of the circle is certainly changed as a consequence and, this done, the circle still passes through O. This is very important as, with O being always on the circle and the position of H unchanged, it follows that the projection of H is also unchanged as are all the other hour marks.
. Let us now turn to the displacement of the sub-style in the equatorial plane. Imagine that we are looking at the figure 4 from the north side of the equator and that the equation of time is positive. We have thus displaced the point C to the left in order to turn the auxiliary circle anti-clockwise. It must be moved sufficiently that the rotation of the radius CH corresponds to the equation of time. The sub-style in the equatorial plane, represented by the line OC, has thus turned by the same angle, but this time clockwise. Lastly, the angle between the style and the sub-style must be adjusted to correspond to the sun's declination.
The choice of position for the point O on the auxiliary circle has the consequence of limiting the duration of use of the sundial during the day. In fact, as has been shown on the page Central projection analemmatic sundials, all the hour marks on the auxiliary circle which are at a greater distance from (I) than O cannot have a useful projection. Lastly, don't forget that the center of projection can be in front of the surface of the sundial or behind it.
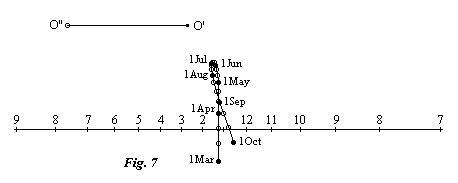
For a practical realization, the most natural way to orientate the style is to keep fixed the point corresponding to the center of projection O and to move the foot of the style along a line marked on the surface of the sundial. This line, which is in the form of a figure 8, is marked with dates.
To illustrate these proposals, here is the dial of a horizontal sundial giving mean time in France, calculated for the following geographic coordinates:
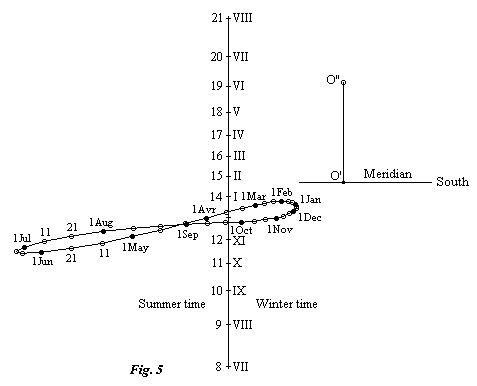
The change from winter time to summer (daylight saving) time is represented by a double numbering of the hour marks. One could, of course, achieve this by a displacement of the style, which gives the following:
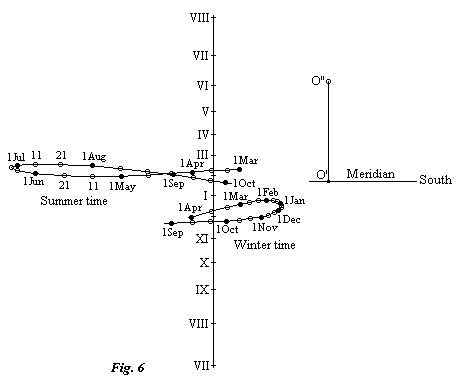
In some particular cases it could be interesting to choose a center of rotation behind the dial surface, although the practical realization of this is difficult. An example is the vertical north-facing sundial of which this is the dial. The figure 8 curve has been truncated because the dial is only lit for positive declinations of the sun. For the same reason, only the hours of summer time are marked.
Date written: 18 November 97
Date translated: 18 February 98