Two mean-time analemmatic sundials

First sundial

Here, then, is the first type of sundial which solves the problem. It is characterised by a direction of projection parallel to the equator. The projection of the auxiliary circle is reduced to a line segment. Figure 1 shows the auxiliary circle (A) with centre C in the equatorial plane. The circle is oriented for zero equation of time.

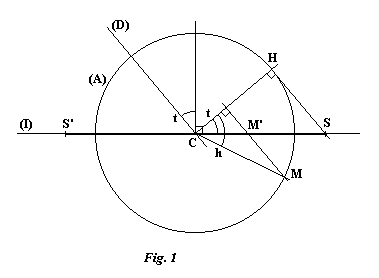
The intersection of the planes of the equator and of the dial surface is represented by the line (I). (D) is the freely chosen direction of projection and SS' is the segment of (I) corresponding to the projection of the auxiliary circle. H is the hour mark on the circle which is projected onto S and t is the angle HCS; t is also the angle between (D) and the perpendicular to (I). Note that CHS is a right angle. The choice of the length s = CS of the half-segment SS' can be seen to force the auxiliary circle's radius to be r0 = s.cos t. The projection of another hour mark such as M, at an angle MCH = h from H, gives the point M' on segment SS'. The distance from M' to C is:

M'C = r0.cos h / cos t
M'C = s.cos h

This is negative when M' is between S' and C.

A line parallel to the earth's axis passes through C, perpendicular to the plane of the figure. The active (shadow-casting) point P of the auxiliary dial is on this axis at a distance PC from C, where:

PC = r0.tan d0
PC = s.cos t.tan d0

where d0 is the sun's declination for the particular date when the equation of time is zero. The style must therefore be positioned through P and parallel to (D).

For a value E of the equation of time, when the circle has been turned by this value, the way to achieve the same projection SS' is to turn the direction of projection by the same angle, so that it remains at right angles to CH (see figure 2).

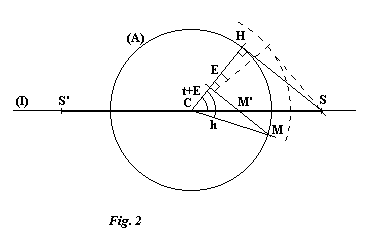
The radius of the auxiliary circle must be changed to r = s.cos (t + E) and we find that M', the projection of M is still at a distance from C given by:

M'C = r.cos h / cos (t + E)
M'C = s.cos h

As for the style, it must be moved along the polar axis by a distance PC = s.cos (t + E).tan d, d being the sun's declination, then turned by an angle E so that it is again parallel to HS.

In practice, making such a sundial is difficult because of this positioning of the style. The ideal support is along the polar axis, as the style always passes through it at right angles. Unfortunately, for a plane dial, the active point on the polar axis is above the plane of the dial for only half the year. It's possible for the polar axis to be in the plane of the dial, which is the case, for example, for Parent's dial. For this, one can imagine a system of markings which show the correct orientation for the style as it moves up and down the polar axis.

Another difficulty inherent in this type of dial is that each point of the segment SS' corresponds to two different times, and there is no simple rule to tell them apart.

Finally, to summarise, let's see how to modify a Parent dial to show mean time. Starting from the initial position, you must:

Turn the style around the polar axis by an angle given by:
```
a = lo + 15.fh + E/4 degrees
```
where:
- lo: Longitude of sundial, positive if west of Greenwich
- fh: time zone, in hours
- E: Equation of time, in minutes, positive if mean time is in advance of sun-time (sun is 'slow')
If a is positive, rotate the style anticlockwise as viewed from the north pole.
Reduce the distance from the style to the equatorial line by the factor f:
```
f = cos (lo + 15.fh + E/4)
f = cos a
```

Return to the main page -o- Second sundial

Date written: 18 November 97
Date translated: 18 February 98