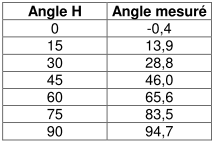
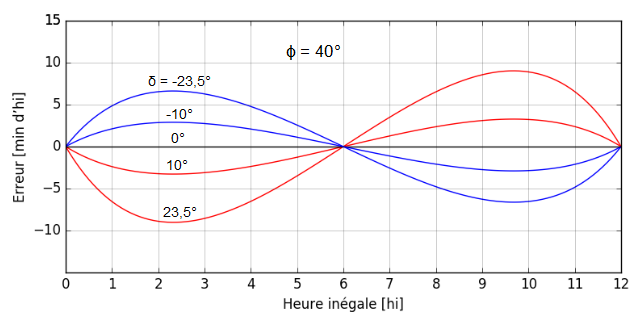
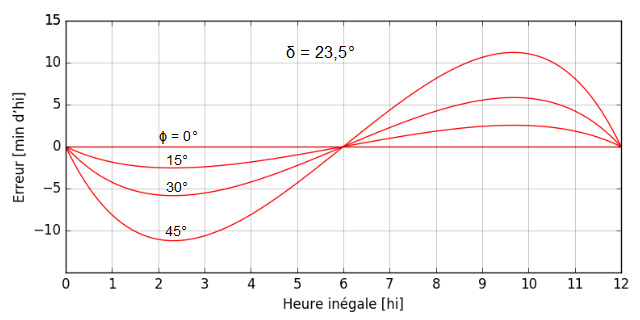
Voici donc la suite de la première partie avec, avant toute chose, une référence que j’ai trouvée entre-temps et qui a le mérite de répertorier tous les cadrans portables romains, universels ou non, avec une carte des lieux où ils ont été retrouvés :
https://shs.cairn.info/revue-du-nord-2012-5-page-97
Abordons maintenant la justification du fonctionnement du cadran universel par la géométrie. Cette approche a déjà fait l’objet de deux publications dont on peut trouver la première, de F. Stebbins en 1958, ici :
https://articles.adsabs.harvard.edu/pdf ... ..52..250S
Bien qu’elle ne s’appuie pas sur un développement rigoureux, elle a le mérite de mettre en place une configuration initiale cohérente et de fournir, en conclusion, une figure donnant une idée correcte de l’approximation obtenue. La seconde publication (
5)
, qui n’est malheureusement pas en accès libre sur Internet, reprend la configuration de la première et, après deux rabattements, utilise la trigonométrie plane pour obtenir l’expression de l’approximation. Ce que je vous présenterai ici est la reprise de la partie géométrique de cette seconde publication avec un complément permettant de retrouver la figure en conclusion de la publication de Stebbins et, de façon plus simple, l’expression de l’approximation.
La figure suivante représente une perspective de la sphère céleste au dessus de l’horizon NESW pour une latitude positive. L’observateur se trouve en O, centre de la sphère céleste. Le méridien est représenté par le demi-cercle SMPN, P étant le pôle Nord. La déclinaison du Soleil est positive et sa course correspond à la portion de cercle LAML’. Elle est centrée sur le point C qui se trouve sur l’axe polaire OP. L’Angle Ho est le demi-angle diurne. Enfin, considérons que le Soleil se trouve en A, son angle horaire est H ou encore l’angle de l’arc MA.
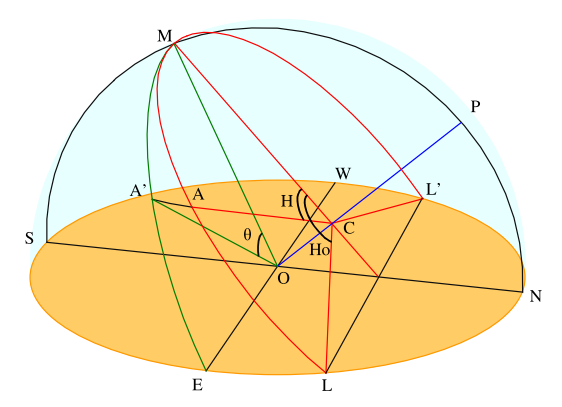Fig. 1 : la sphère céleste en perspective
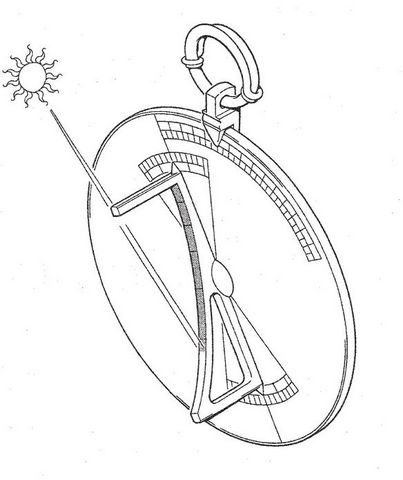
Intéressons-nous maintenant à la mesure du cadran romain en sachant que son réglage est tel que, quand il est suspendu et que le disque du cadran est dans le plan du méridien, l’axe du porte-ombre amovible est dirigé vers la position du Soleil à midi vrai, ainsi le quart de plan défini par le porte-ombre et son échelle de mesure dessine sur la sphère un quart de grand cercle, représenté en vert sur la figure, qui passe par les points M et E. Suivant le mode d’utilisation du cadran, il faut que le Soleil soit situé dans ce quart de plan, ce qui s’obtient en faisant tourner le cadran autour de l’axe vertical. Dans le cadre de notre figure, ce qui reviendra au même, c’est le Soleil que nous allons reporter de A en A’, par rotation autours de l’axe vertical. La mesure, qui consiste à évaluer la position de A’ sur le quart de cercle EM, utilise donc la hauteur du Soleil sur l’horizon d’où la classification indiquée dans la première partie. Par similitude avec l’angle horaire H et par commodité pour l’évaluation finale, la position A’ sera repérée par l’angle de l’arc MA’, ou encore l’angle θ.
Plaçons-nous, figure suivante, dans le plan du méridien et intéressons-nous à la projection orthogonale des éléments de la sphère sur ce plan, c’est-a-dire utilisons la technique ancienne connue sous le nom d’analemme (
6)
.
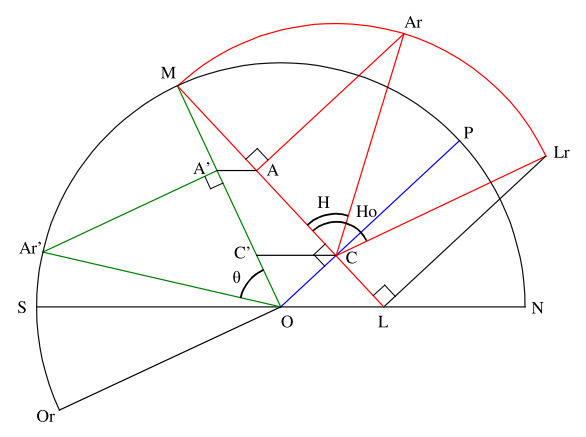Fig. 2 : projection de la sphère céleste sur le méridien et rabattements
On retrouve le demi-cercle SMPN du méridien et le diamètre SN passant par le centre O. Le segment ML est la trace de la course diurne du Soleil, elle est perpendiculaire à l’axe polaire OP. Pour trouver la position A du Soleil sur cette trace, rabattons autours de celle-ci la portion de cercle MAL de la figure 1. On peut tracer facilement ce rabattement en tirant du centre C un cercle passant par M puis en traçant les rayons CAr et CLr faisant respectivement les angles H et Ho avec CM. De Ar, il suffit de descendre une perpendiculaire à ML pour obtenir le point A.
Le rayon OM est la trace du quart de plan correspondant au porte-ombre amovible. Pour trouver l’angle mesuré nous allons rabattre la portion de cercle MA’E de la figure 1 autour de OM pour obtenir le quart de cercle MSOr qui se confond en partie avec le demi-cercle du méridien. À présent, pour obtenir l’angle θ mesuré, il suffit de reporter A sur le rayon OM en traçant une parallèle à SN et, du point A’ obtenu, tirer une perpendiculaire à OM pour obtenir le point Ar’, l’angle θ est la mesure de l’arc MAr’.
Cette figure a l’avantage de représenter sur un même plan, d’un côté en rouge, la course du Soleil et de l’autre, en vert, la mesure effectuée par le cadran. Pour que le comparaison soit encore plus facile, remarquons que les angles H et Ho sont entièrement définis par les rapports respectifs de CA et CL à CM (qui correspondent en terme moderne aux cosinus de H et Ho). Si nous reportons le point C en C’ par une ligne parallèle à SN, d’après le théorème de Thalès, nous retrouvons les mêmes rapports avec C’A’, C’O et C’M. En d’autres termes, nous pouvons compresser et déplacer la partie rouge de la figure pour venir « coller » le segment ML sur MO tout en conservant les angles H et Ho. On obtient ainsi la figure 3 suivante qui a l’avantage supplémentaire d’être plus simple.
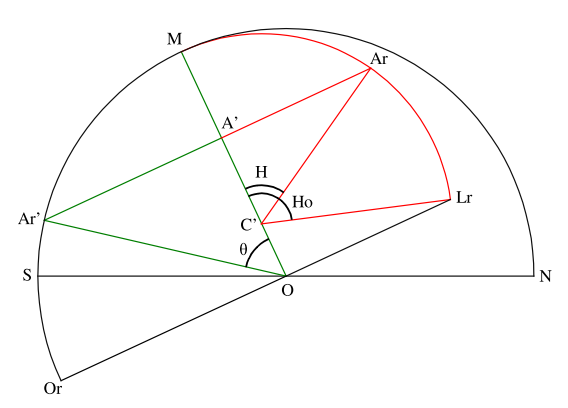Fig. 3 : relation entre θ, H et Ho pour une déclinaison positive
Le même exercice avec une déclinaison du Soleil négative, en inversant les parties rouge et verte, donne la figure 4 suivante. Dans celle-ci la partie rouge a été dilatée.
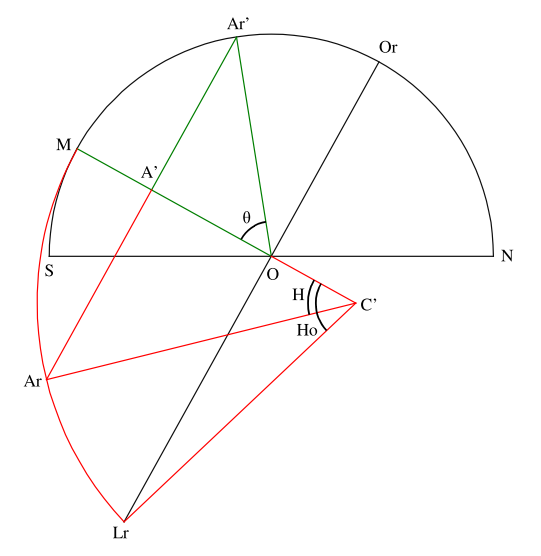Fig. 4 : relation entre θ, H et Ho pour une déclinaison négative
On comprendra facilement que si la déclinaison est nulle, les points O, C et L de la figure 2 sont confondus. Il s’en suit que Ho = 90°, les parties rouge et verte sont identiques et que θ = H.
Rassemblons à la figure 5 les différents arcs semi-diurnes des déclinaisons positive, négative et nulle du Soleil.
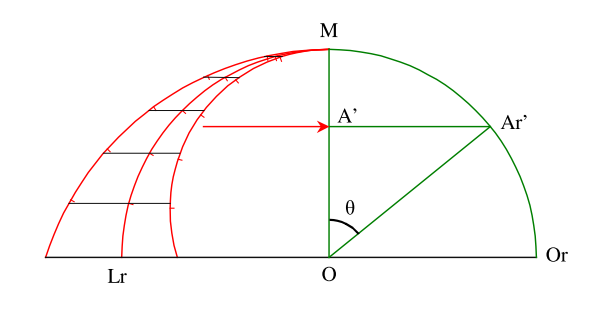Fig. 5 : compromis de la graduation de θ pour toutes les déclinaisons
Le principe des heures inégales est de découper la journée en 12 durées égales ou, ce qui revient au même, la course semi-diurne du Soleil en 6 parties égales. Ces divisions ont été tracées à la figure 5 et elles font apparaître qu’un compromis intéressant pour la graduation de l’échelle de mesure de θ est la division du quart de cercle MAr’Or en 6 partie égales de 15°, ce qui permet notamment d’avoir une erreur nulle aux équinoxes.
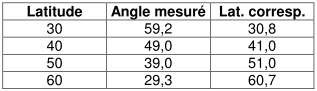
Comme indiqué dans l’introduction de ce message, on retrouve en conclusion de la publication de F. Stebbins la figure suivante qui est similaire à la figure 5, mais organisée différemment.
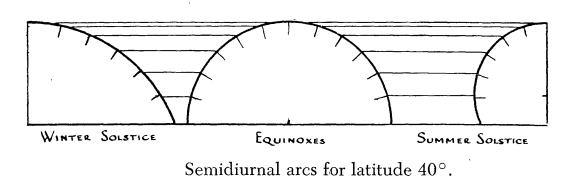
La figure 5 apparaît aussi sous une autre forme dans le postulat de l’approximation qui a permis de trouver la géométrie d’un cadran à lignes horaires parallèles puis celle du quadrant ancien dans ce sujet :
viewtopic.php?t=121
Il est effectivement assez curieux de remarquer que le cadran romain universel et le quadrant ancien, qui sont de forme et d’utilisation entièrement différentes, reposent rigoureusement sur la même base d’approximation.
Je vous laisse le temps de bien comprendre ce que je vous ai présenté et, éventuellement, me poser des questions si certains points n’étaient pas suffisamment clairs avant d’aborder dans une prochaine partie les aspects trigonométriques qui permettront de quantifier l’approximation.
(5)
^ M. T. Wright : Greek and Roman Portable Sundials. An Ancient Essay in Approximation, 2000. Dans Archive for History of Exact Sciences, t. 55, p. 177-187
(6)
^ Voir De l’Analemme aux cadrans de hauteur, Y. Massé, 2009 disponible ici :
Contenu réservé aux adhérents connectés.
