Comme proposé, voici un développement plus important au sujet de la course du Soleil prenant en compte la variation de la déclinaison. Cette variation est généralement négligée en gnomonique mais elle prend toute son importance dans le cadre l’énigme. On peut consulter avec profit cette
publication d’Alexandre Vial qui quantifie l’angle horaire de culmination du Soleil et la différence de hauteur entre la culmination et le passage au méridien. Les deux relations qu’il obtient sont :
sin Hc = Δδ.(tan ϕ – tan δ)
dh = cos h0.Δδ²/(2.cos ϕ.cos δ)
Avec :
- Hc : angle horaire de la culmination
- δ : déclinaison du soleil
- Δδ : grandeur sans dimension correspondant à la variation de δ par angle horaire.
- ϕ : latitude du lieu d’observation
- dh : différence de hauteur entre culmination et passage au méridien
- h0 : hauteur du Soleil à midi solaire
Bien que ces formules soient données en considérant l’angle horaire de culmination faible, j’ai pu constater expérimentalement qu’elles donnaient une bonne approximation quand il est de quelques heures. Comme le souligne Stéphane, les angles horaires importants ne peuvent être obtenus que pour des latitudes élevées, disons supérieures à 89° et en dehors de la période des solstices, ce qui est le cas pour notre énigme car pour avoir un Soleil qui se lève et se couche à proximité du pôle il faut que sa déclinaison soit proche de 0°. Dans ce cas, on peut même simplifier la première relation car tan δ devient négligeable par rapport à tan ϕ, on obtient donc :
sin Hc = Δδ.tan ϕ
Bien que cela ne soit pas mentionné dans l’étude d’A. Vial, cette relation étant la solution d’une recherche d’extremum, elle permet aussi de déterminer l’instant où le Soleil est au plus bas dans sa course. En effet, pour un sinus donné il y a deux angles possibles, le second étant l’angle horaire Hi du passage au minimum de hauteur :
Hi = 180° – asin(Δδ.tan ϕ) (
1)
Cette relation nous permet aussi de déterminer la latitude au delà de laquelle il ne sera plus possible d’avoir un coucher suivi par un lever, c’est-à-dire en absence d’extremum ou encore pour :
Δδ.tan ϕ > 1
À la période des équinoxes, la variation de déclinaison par jour est de 0,395°, d’où Δδ = 0.395/360 = 0,0011 et ϕ > 89,973°, ce qui correspond à une région circulaire de 7 km de rayon autour du pôle.
Pour illustrer ces considérations théoriques, voyons ce qui s’est passé le 18 mars 2024 à la longitude de 52° E en utilisant un calcul d’éphéméride simplifié. À la latitude de 89,5° (à 55 km du pôle nord) voici l’évolution de la hauteur au cours de la journée solaire :
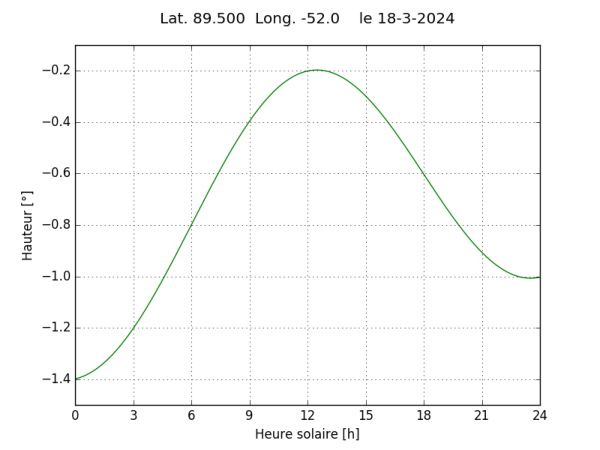
La culmination se produit à 12 h 29, la variation de hauteur pendant les 29 min qui suivent midi est de 0,004°. En comparaison la parallaxe du Soleil est de 0,0024°, valeur toujours négligée en gnomonique et généralement négligée en navigation astronomique. On voit qu’on est dans l’épaisseur du trait et bien qu’on puisse trouver pour cette latitude (comme pour des latitudes plus faibles), en se déplaçant en longitude, des conditions où la hauteur du Soleil passe par -0,6° deux fois dans l’après-midi, ce qui répond à l’énigme, il faut reconnaître qu’on s’éloigne de plus en plus d’une « réalité sensible ».
Notons que la hauteur minimale de la seconde partie de la journée est atteinte, symétriquement, 29 min avant minuit (il ne faut pas considérer la hauteur plus faible de –1,4° à 0 h comme un extremum car la tangente à la courbe n’est pas horizontale, l’extremum correspondant a été atteint à la fin de la journée précédente). On peut aussi noter la différence de hauteur d’environ 0,4° entre 0 et 24 h qui correspond à la variation de la déclinaison du Soleil sur la journée et qu’on retrouvera sur toutes les courbes suivantes.
Déplaçons nous directement à la latitude limite de 89,937° où on obtient la courbe suivante :
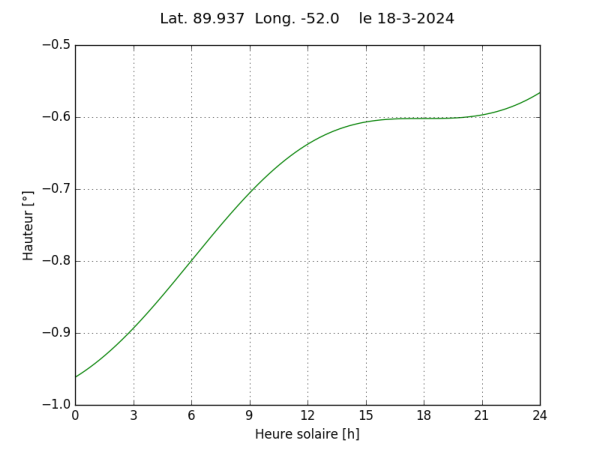
On constate que les deux extremums se rejoignent à 18 h en un point d’inflexion. La variation de hauteur entre le « plateau » et midi ou minuit est maximale, elle n’est toutefois que de 0,0395° (la formule d’A. Vial donne 0,0314°).
Si on se place au pôle, la hauteur du Soleil correspond à sa déclinaison et on obtient sans surprise une évolution pratiquement linéaire de la hauteur.
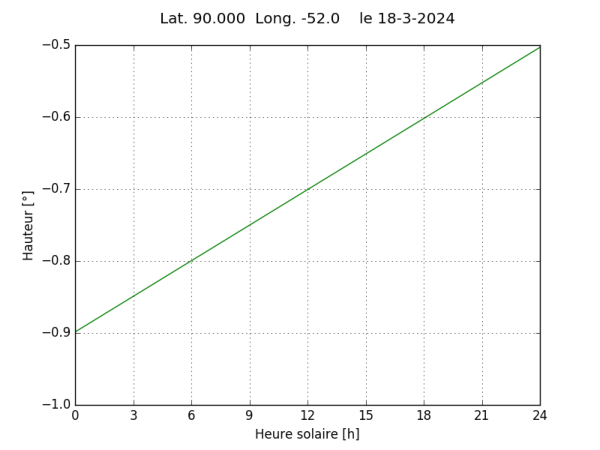
Plaçons nous maintenant à la latitude particulière ϕs pour laquelle Hc est proche de 45° ou 15 h solaire. Sa valeur s’obtient simplement par la relation ϕs = atan(sin 45°/Δδ). On obtient ϕs = 89,91°, valeur proche de celle proposée par Stéphane. On est donc situé à 10 km du pôle et on obtient la courbe suivante :
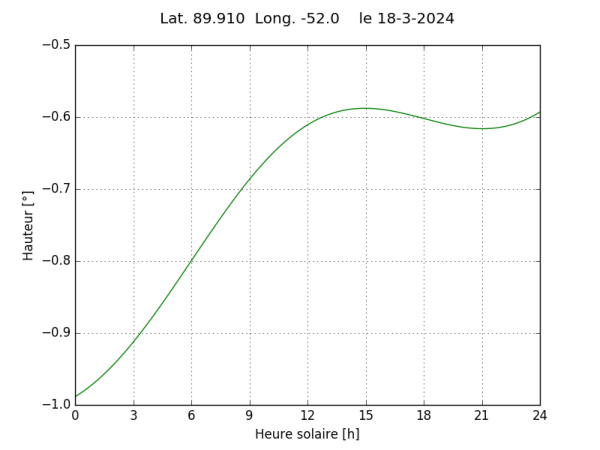
Le choix qui a été fait de la longitude permet d’obtenir les lever et coucher répondant à l’énigme avec une curieuse surprise : un second lever dans la seconde moitié de la journée ! Cette succession d’événements sera toutefois éphémère car, pour le même lieu, le prochain coucher n’interviendra que 6 mois plus tard, quant au prochain lever ce sera l’année suivante...
La consultation des
éphémérides de l’IMCCE, bien plus précises, permet de confirmer les valeurs suivantes :
- À midi solaire h0 = -0,6115°
- Lever à 12 h 49
- Culmination à 14 h 57 (la formule d’A. Vial donne la même valeur) avec h = -0,5884° soit une variation dh = 0,0231° (la formule d’A. Vial donne 0,022°)
- Coucher à 17 h 38
- Nouveau lever à 23 h 35
Encore une fois, on voit qu’on est sur des variations infimes de hauteur (dh est inférieur au vingtième du diamètre apparent du Soleil) et décelables uniquement par des instruments précis. En conséquence la solution à l’énigme n’est qu’une simple considération théorique, pratiquement indétectable par un observateur humain.
Notons pour conclure que l’énigme aurait pu être proposée, symétriquement, de la façon suivante : dans quelle condition le Soleil se couche deux fois dans la même journée avant midi. Une des réponses possibles est celle indiquée par le titre de la courbe suivante :
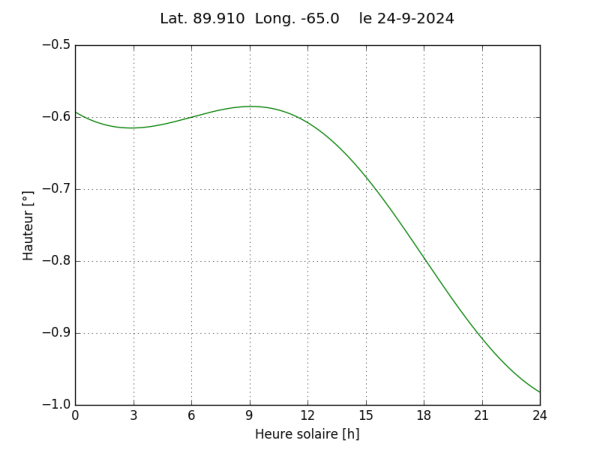 Note :
Note :
1
^ - dans le cas où tan δ ne peut pas être négligé, le calcul de Hi doit se faire par la relation :
Hi = 360° - asin(Δδ.(tan ϕ + tan δ))
car, dans ce cas, cos Hi = -1




