Énigme : une propriété du cadran analemmatique

[Yvon_M]

À la fin de son article sur la généralisation du cadran annalematique (que je cite toujours volontiers comme un exemple de concision), Peaucellier énonce, sans démonstration, une propriété propre aux cadrans classiques - c’est-à-dire horizontaux avec un style vertical - concernant l’heure de coucher du Soleil :
« On s’assure aisément que le coucher du Soleil répond à une normale menée à l’ellipse par le point de déclinaison. »

Ce qui signifie que si l’on prend une droite tangente à l’ellipse dont le point de contact corresponde à une heure de coucher du Soleil, la perpendiculaire à la tangente passant par le point de contact passe par la date concernée au niveau de l’échelle des dates. Bien sûr, ceci est aussi valable pour l’heure de lever.

Sauriez-vous démontrer cette particularité de façon aussi expéditive que Peaucellier avec quelques propriétés géométriques ?

Pour information, voici une des propriétés à utiliser :
La projection de la tangente à une courbe est une droite tangente à la courbe projetée.

[Stéphane_L]

Je propose :
L’ellipse des cadrans analemmatiques est une projection de l’équateur d'une sphère armillaire centrée sur un point dont la projection orthogonale est le centre de l’ellipse.
• Soit d1 la tangente à l’équateur passant par l’heure solaire.
• Soit P1 le plan \(\perp\) à l’horizon contenant d1.
• Soit d2 la demi-droite d’origine le soleil (rayon du soleil) passant par le sommet du gnomon.
• Soit P2 contenant d2 et l’axe de la sphère. On a P2\(\perp\)P1.
Donc à l’heure du lever (ou du coucher) d2\(\perp\)P1 car d2 est horizontale.
• La projection orthogonale de d2 sur l’horizon est \(\perp\) à l’intersection de P1 avec l’horizon qui est aussi (cf. propriété) tangente à l’ellipse du cadran passant par l’heure du lever (ou du coucher) .
• Comme la projection orthogonale de d2 sur l’horizon passe par le pied du gnomon (date) on obtient bien la propriété par Peaucellier.

[Yvon_M]

Oui Stéphane, cette démonstration est parfaitement correcte et donne entièrement l’explication de cette propriété assez curieuse.

Au 4e point, j’ai toutefois eu du mal à me convaincre de l’affirmation P2 \(\perp\) P1. Elle est peut-être plus facile à comprendre si on détaille : P2 passe par l’axe de la sphère et le point horaire de l’équateur, donc P2 \(\perp\) d1. Comme d1 appartient à P1, alors P1 \(\perp\) P2.

Attaquons-nous maintenant à l’énigme que nous a proposé sebB…

[Yvon_M]

J. H. Lambert avait lui-aussi remarqué et consigné cette surprenante propriété dans ses « Beyträge » (dont je vous ai proposé une traduction) mais il l’avait aussi complétée, sans démonstration, par une autre propriété tout aussi curieuse qui se trouve dans la première partie de la page 320 :

« Il est inutile de préciser ici que les points L, F, G, f et l se trouvent tous sur la circonférence d’un cercle, car cela découle du fait que GL, Gl sont des lignes normales. »

L et l étant les heures de lever et coucher du Soleil à la date correspondant au point G ; F et f les foyers de l’ellipse. On a d’ailleurs baptisé cette circonférence : cercle de Lambert.



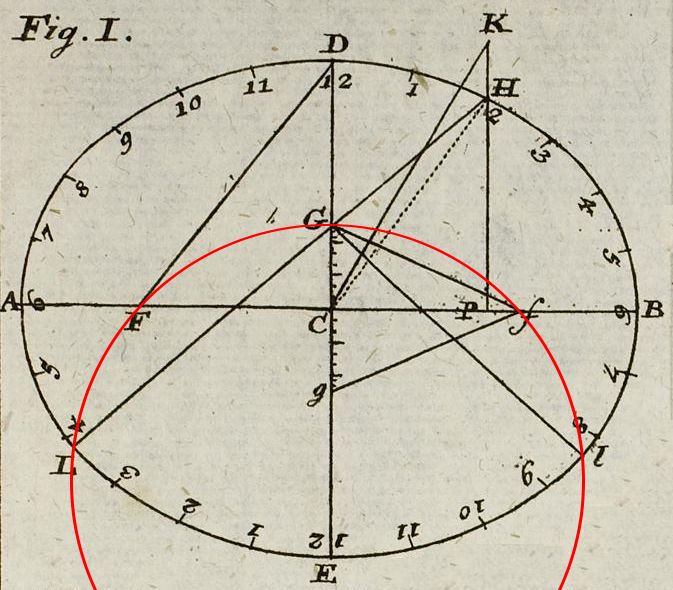
Sauriez-vous donner une justification géométrique à cette nouvelle propriété ? J’avoue que je n’ai pas réussi à la trouver sans rechercher dans les écrits à ce sujet mais, en soi, elle n’est pas très compliquée quand on fait appel à deux propriétés essentielles, une propre au cercle et l’autre à l’ellipse.

[Stéphane_L]

Curieuse propriété en effet!
Voici ma proposition :

cercle de Lambert.png (46.5 Kio) Vu 26506 fois

D'après la propriété de réflexivité de l'ellipse on a F'LG = GLF .
Notons mes(FLG) = mes(F'LG) = l ; mes(GF'L) = f' ; mes(GFL) = f

D'après la propriété des sinus :
dans le triangle GF'L : sinl/GF' = sinf'/GL
dans le triangle FGL : sinl/FG = sinf/GL

F et F' étant symétriques par rapport à (CG), on a GF = GF' donc sinf = sinf' d’où f = π - f'.
Donc FGF'L sont cocycliques (d'après la réciproque du théorème de cocyclicité).
De même F'GFL' cocycliques.
Donc L'FGF’L sont cocycliques.

[Yvon_M]

Bravo Stéphane, la justification est parfaitement correcte. On peut toutefois faire légèrement plus simple et n’utiliser que des propriétés géométriques. Celle de l’ellipse est bien la réflexivité que vous avez indiquée et qui fait que les angles FL’G et GL’F’ d’un côté, FLG et GLF’ de l’autre, sont identiques.

Quant au cercle, on peut utiliser la propriété qui fait qu’une corde est vue sous le même angle pour tous les points du cercle situés du même coté de la corde.

Ainsi, si on trace le cercle passant par F, G et F’, les cordes FG et GF’ étant identiques par symétrie, en tout point M du cercle situé de l’autre côté de la droite FF’ par rapport à G, les angles FMG et GMF’ sont identiques. L’intersection du cercle avec l’ellipse ne peut donc se faire qu’aux points L’ et L.

Comme nous l’a fait remarquer Jean-Marie_M, Lambert était vraiment un autodidacte étonnant…