La réfraction est un phénomène dû à l’atmosphère terrestre qui est traversée par les rayons lumineux provenant des différents corps célestes. Ils sont alors vus un peu plus haut que leur réelle position. La différence entre la position apparente et la position réelle est d’autant plus importante que l’astre est bas sur l’horizon. Au zénith il n’y a pas d’effet de réfraction, à 45° de hauteur la réfraction est de l’ordre de 1’ (une minute d’arc) et sur l’horizon elle atteint environ 50’. Cette dernière valeur est supérieure au diamètre du Soleil (32’) si bien qu’il est déjà couché quand, par exemple, nous le voyons toucher l’horizon.
La réfraction varie en fonction de la couleur des rayons lumineux et des conditions météorologiques (température, pression et hygrométrie). Ces variations sont d’autant plus importantes que la hauteur observée est faible et elles deviennent difficilement prévisibles près de l’horizon. On peut le constater facilement en observant le Soleil couchant qui prend nominalement une forme aplatie car son bord inférieur est plus relevé par le réfraction que son bord supérieur. En pratique, on constate couramment des formes beaucoup plus complexes car les couches atmosphériques traversées sont plus étendues géographiquement et sont susceptibles de plus d’irrégularités en fonction de la variation locale des conditions météorologiques.
Dans cette contribution nous ne prendrons en compte que les hauteurs supérieures à 20° en ne considérant que des conditions météorologiques moyennes. Dans ce cas on peut avoir une estimation de l’angle \(r\) entre la position observée d’un astre et sa position réelle par la relation \(r = \alpha\cdot\cot h\) (1), \(h\) étant la hauteur de l’astre et \(\alpha\) un angle de 1’ ou encore 4 secondes de temps.
Pour évaluer l’impact de la réfraction sur l’angle horaire, considérons le triangle sphérique de la sphère céleste, appelé triangle de position, qui a pour sommets le pôle nord \(P\), le zénith \(Z\) et le Soleil réel \(S\).
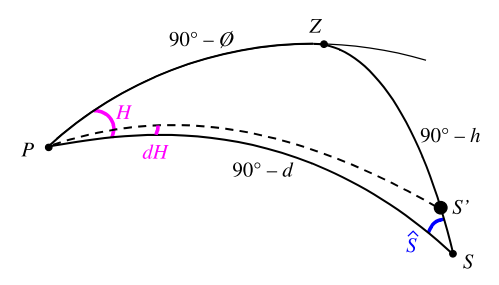
Entre les points \(P\), \(Z\) et \(S\) on a les angles suivants :
- \(PZ = 90°- \phi\), \(\phi\) étant la latitude du lieu considéré
- \(PS = 90°- d\), \(d\) étant la déclinaison du Soleil
- \(ZS = 90°- h\), \(h\) étant la hauteur du Soleil
Dans le triangle \(PSS'\), nous avons par la loi des sinus :
\(\frac{\sin dH}{\sin r}=\frac{\sin\hat{S}}{\sin PS'}\)
\(r\) et \(dH\) étant faibles, on peut écrire \(PS'\simeq PS = 90°-d\) , ainsi :
\(\frac{\sin dH}{\sin r}\simeq\frac{dH}{r}\simeq\frac{\sin\hat{S}}{\cos d}\) d’où \(dH\simeq\frac{\sin\hat{S}}{\cos d}\cdot r\) (2)
La loi des sinus dans le triangle \(PZS\) nous donne :
\(\frac{\sin\hat{S}}{\cos\phi}=\frac{\sin H}{\cos h}\) d’où \(\sin\hat{S}=\frac{\sin H}{\cos h}\cdot\cos\phi\) (3)
En remplaçant \(\sin\hat{S}\) (3) et \(r\) (1) dans (2) on obtient :
\(dH=\frac{\sin H\cdot\cos\phi}{\cos h\cdot\cos d}\cdot\alpha\cdot\cot h=\frac{\sin H\cdot\cos\phi}{\sin h\cdot\cos d}\cdot\alpha\)
Enfin en utilisant la formule de la hauteur : \(\sin h=\sin d\cdot\sin\phi+\cos d\cdot\cos\phi\cdot\cos H\)
\(dH=\frac{\sin H\cdot\cos\phi}{(\sin d\cdot\sin\phi+\cos d\cdot\cos\phi\cdot\cos H)\cos d}\cdot\alpha\)
Puis en simplifiant par \(\cos\phi\) :
\(dH=\frac{\sin H}{(\sin d\cdot\tan\phi+\cos d\cdot\cos H)\cos d}\cdot\alpha\)
C’est la relation cherchée qui donne l’erreur \(dH\) en fonction de l’angle horaire, la latitude et la déclinaison du Soleil. On peut d’emblée constater que l’erreur est nulle à midi vrai, ainsi les méridiennes ne sont pas concernées par l’erreur apportée par la réfraction.
Une autre propriété curieuse de cette relation apparaît à la période des équinoxes. En effet, pour \(d\) = 0 la relation devient :
\(dH=\frac{\sin H}{\cos H}\cdot\alpha=\alpha\cdot\tan H\)
L’erreur \(dH\) est dans ce cas indépendante de la latitude. De plus on peut facilement la calculer pour les instants de 9 et 15 h vraie car \(\tan H\) = 1 et par suite \(dH\) = 4 s. Cette valeur est significative de l’ordre de grandeur propre à l’erreur introduite par la réfraction et donne la limite de précision que peut atteindre un cadran solaire d’angle horaire s’il n’introduit pas de correction propre à la réfraction.
On peut se référer avec profit à l’article Réfraction et gnomonique de Gérard Baillet paru dans Cadran-Info n° 26, p. 5 :
https://ccs.saf-astronomie.fr/wp-conten ... nfo_26.pdf
On retrouve dans cet article des courbes erreur = f(heure vraie) calculées avec précision pour différentes latitudes, elles sont très proches de celles qu’on peut obtenir avec la relation établie dans cette contribution.