Oui, Seb, il faut effectivement considérer que la planchette a une orientation absolument quelconque. De plus, on a aucune idée de la façon dont le gnomoniste a disposé les axes du repère, c’est-à-dire dans quel sens on passe du premier axe au second : horaire ou anti-horaire ?
Aussi surprenant que cela puisse paraître, il est vraiment possible de trouver la solution avec aussi peu de précisions. S’il y a d’autres personnes qui veulent tenter de la trouver, voici quelques indications complémentaires : les deux résolutions dont j’ai parlé plus haut sont successivement celle d’un triangle plan et celle d’un triangle sphérique.
Allez, s’il n’y a pas de proposition avant dimanche prochain, je vous donnerai la réponse à ce moment là.
Bonne semaine !
Énigme : la planchette du gnomoniste
- Yvon_M
- Administrateur du site
- Messages : 348
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Énigme : la planchette du gnomoniste
Yvon Massé - Site perso. : La gnomonique
-
Stéphane_L
- Messages : 95
- Enregistré le : lun. 3 juin 2019 21:33
Re: Énigme : la planchette du gnomoniste
Bonsoir,
Je proposerais,
Inclinaison : 42,32°
Déclinaison : - 36,52°
Donc la montre du gnomoniste (réglée sur l’heure solaire) indique 6h 23m.
Je proposerais,
Inclinaison : 42,32°
Déclinaison : - 36,52°
Donc la montre du gnomoniste (réglée sur l’heure solaire) indique 6h 23m.
- Yvon_M
- Administrateur du site
- Messages : 348
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Énigme : la planchette du gnomoniste
Désolé, Stéphane, ce n’est pas la bonne réponse. En fait, j’aurais dû le préciser, j’ai considéré que la montre du gnomoniste était réglée sur l’heure légale comme celle de tous ses contemporains. Dans ce cas, l’heure à trouver peut se calculer de la façon suivante.
Pour commencer, donnons des noms aux différentes positions ou grandeurs que nous allons utiliser : \(K\) pour l’extrémité du gnomom ; \(g\) sa longueur ; \(P_1\), \(P_2\) pour les positions de l’ombre relevées par notre gnomoniste aux coordonnées \(x_1\), \(y_1\) puis \(x_2\), \(y_2\) ; \(S_1\), \(S_2\) pour les positions du Soleil aux moment correspondants et \(t_1\), \(t_2\) ces instants.
Nous ne savons effectivement que peu de choses sur la planchette mais nous pouvons calculer la distance entre \(P_1\) et \(P_2\) car le repère est orthogonal et on peut constater que la relation est valable quelque soit le sens pour passer du premier axe au second.
\(P_1P_2 = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} = \sqrt{(188 + 12)^2 + (76 - 34)^2} = 204,4\) mm
De la même façon nous pouvons calculer la distance entre le point \(K\) et les points \(P_1\) ou \(P_2\) car le centre du repère est au pied du gnomon.
\(KP_1 = \sqrt{g^2 + x_1^2 + y_1^2} = \sqrt{120^2 + 12^2 + 34^2} = 125,3\) mm
\(KP_2 = \sqrt{g^2 + x_2^2 + y_2^2} = \sqrt{120^2 + 188^2 + 76^2} = 235,6\) mm
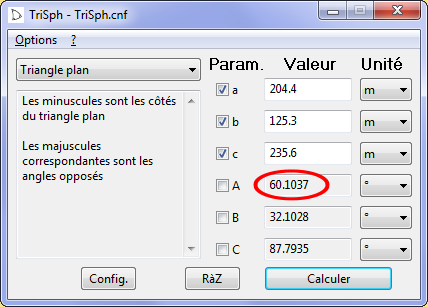
Les 3 points \(P_1\), \(P_2\) et \(K\) forment un triangle dont nous connaissons les 3 côtés, nous pouvons donc calculer ses 3 angles et il y en a un qui nous intéresse particulièrement : c’est l’angle en \(K\) car, la planchette n’ayant pas bougé, il correspond à l’angle entre \(S_1\) et \(S_2\).
Le formulaire de résolution des triangles est connu, c’est par essence le fondement de la trigonométrie (voir par exemple : https://fr.wikipedia.org/wiki/Résolutio ... n_triangle). On peut aussi utiliser des programmes qui se trouvent facilement sur Internet pour les résoudre. J’utiliserai ici celui que je connais le mieux, TriSph, qui nous donne : \(K = 60,1°\)
J’avais suggéré à Seb de prendre de la hauteur, faisons-le pour regarder la sphère céleste d’en haut et considérer sur celle-ci les positions du Soleil \(S_1\), \(S_2\) et le pôle nord \(N\). Étant donné que nous connaissons les dates des instants \(t_1\) et \(t_2\) nous pouvons calculer les angles \(NS_1\) et \(NS_2\) qui correspondent respectivement à \(90° - d_1\) et \(90°- d_2\), \(d_1\) et \(d_2\) étant les déclinaisons du Soleil aux instants \(t_1\) et \(t_2\).
Nous pouvons même obtenir des valeurs relativement précises en observant que les coordonnées du chantier de notre gnomoniste correspondent à un lieu situé en France, ce qui nous permet de connaître la relation entre l’heure légale et le temps universel et ainsi extraire précisément les déclinaisons des éphémérides. Si, d’un côté, nous connaissons exactement l’heure légale de \(t_1\), l’heure approximative de \(t_2\), « à la première heure », nous suffira pour obtenir la valeur de \(d_2\) avec une précision suffisante en prenant par exemple \(7\) h. Notons au passage que notre énigme se situe en 2010 et que, depuis 1976 en France, un changement d’heure est appliqué en été. Il s’effectue le dernier weekend de mars, donc entre \(t_1\) et \(t_2\). En prenant toutes ces données en compte nous obtenons à partir des éphémérides :
\(d_1 = -0,91°\) d’où \(NS_1 = 90,91°\)
\(d_2 = 7,16°\) d’où \(NS_2 = 82,84°\)
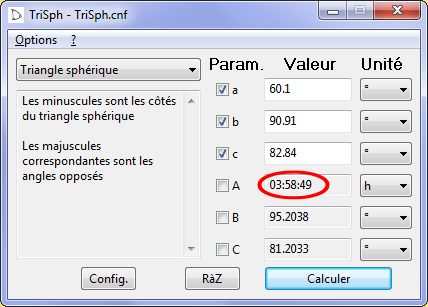
Les 3 points \(S_1\), \(S_2\) et \(N\) forment un triangle sphérique dont nous connaissons maintenant les 3 côtés et nous pouvons calculer l’angle en \(N\) qui représente la différence des heures solaires aux instants \(t_1\) et \(t_2\). TriSph nous donne cet angle directement en heure : \(N = 3\) h \(58\) min \(49\) s
Pour passer de l’heure légale \(hl_1\) et \(hl_2\) à l’heure solaire aux instants \(t_1\) et \(t_2\) nous avons besoin des équations du temps \(et_1\) et \(et_2\). Comme pour la déclinaison, \(et_1\) s’obtient précisément sachant que \(t_1\) est parfaitement défini et \(et_2\) peut s’obtenir avec une précision suffisante en partant d’une valeur approchée de \(t_2\). En prenant \(7\) h pour l’heure légale de \(t_2\), les éphémérides nous donnent :
\(et_1 = 8\) min \(6\) s
\(et_2 = 1\) min \(57\) s
Sachant enfin que notre gnomoniste retourne sur son chantier plus tôt qu’il l’a quitté et en appelant \(cl\) la correction de longitude, nous pouvons écrire :
\((hl_1 – et_1 – cl – 1\) h\() – (hl_2 – et_2 – cl – 2\) h\() = N\)
d’où \(hl_2 = hl_1 – et_1 + et_2 + 1\) h \(– N\)
\(hl_2 = 11\):\(12\):\(00 - 00\):\(08\):\(06 + 00\):\(01\):\(57 + 1\):\(00\):\(00 - 3\):\(58\):\(49 = 8\):\(07\):\(02\)
Au retour de notre gnomoniste sur son chantier, sa montre indique donc \(8\) h \(7\) min
Remarquons que, curieusement, nous avons obtenu ce résultat sans utiliser les valeurs numériques de la position géographique ni avoir recours à l’orientation de la planchette, ces grandeurs étant généralement jugées indispensables en gnomonique. Cet apriori nous conduirait, dans ce cas, à des équations inextricables.
Si, comme l’a supposé Stéphane, la montre du gnomoniste avait été réglée sur l’heure solaire, les déclinaisons obtenues ci-dessus peuvent toujours être considérées comme justes ainsi que le calcul qui les utilise, l’angle en \(N\). Il n’y a donc à reconsidérer que le dernier calcul qui s’écrit alors plus simplement :
\(hs_2 = hs_1 – N = 11\):\(12\):\(00 - 3\):\(58\):\(49 = 7\):\(13\):\(11\)
Pour commencer, donnons des noms aux différentes positions ou grandeurs que nous allons utiliser : \(K\) pour l’extrémité du gnomom ; \(g\) sa longueur ; \(P_1\), \(P_2\) pour les positions de l’ombre relevées par notre gnomoniste aux coordonnées \(x_1\), \(y_1\) puis \(x_2\), \(y_2\) ; \(S_1\), \(S_2\) pour les positions du Soleil aux moment correspondants et \(t_1\), \(t_2\) ces instants.
Nous ne savons effectivement que peu de choses sur la planchette mais nous pouvons calculer la distance entre \(P_1\) et \(P_2\) car le repère est orthogonal et on peut constater que la relation est valable quelque soit le sens pour passer du premier axe au second.
\(P_1P_2 = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} = \sqrt{(188 + 12)^2 + (76 - 34)^2} = 204,4\) mm
De la même façon nous pouvons calculer la distance entre le point \(K\) et les points \(P_1\) ou \(P_2\) car le centre du repère est au pied du gnomon.
\(KP_1 = \sqrt{g^2 + x_1^2 + y_1^2} = \sqrt{120^2 + 12^2 + 34^2} = 125,3\) mm
\(KP_2 = \sqrt{g^2 + x_2^2 + y_2^2} = \sqrt{120^2 + 188^2 + 76^2} = 235,6\) mm
Les 3 points \(P_1\), \(P_2\) et \(K\) forment un triangle dont nous connaissons les 3 côtés, nous pouvons donc calculer ses 3 angles et il y en a un qui nous intéresse particulièrement : c’est l’angle en \(K\) car, la planchette n’ayant pas bougé, il correspond à l’angle entre \(S_1\) et \(S_2\).
Le formulaire de résolution des triangles est connu, c’est par essence le fondement de la trigonométrie (voir par exemple : https://fr.wikipedia.org/wiki/Résolutio ... n_triangle). On peut aussi utiliser des programmes qui se trouvent facilement sur Internet pour les résoudre. J’utiliserai ici celui que je connais le mieux, TriSph, qui nous donne : \(K = 60,1°\)

J’avais suggéré à Seb de prendre de la hauteur, faisons-le pour regarder la sphère céleste d’en haut et considérer sur celle-ci les positions du Soleil \(S_1\), \(S_2\) et le pôle nord \(N\). Étant donné que nous connaissons les dates des instants \(t_1\) et \(t_2\) nous pouvons calculer les angles \(NS_1\) et \(NS_2\) qui correspondent respectivement à \(90° - d_1\) et \(90°- d_2\), \(d_1\) et \(d_2\) étant les déclinaisons du Soleil aux instants \(t_1\) et \(t_2\).
Nous pouvons même obtenir des valeurs relativement précises en observant que les coordonnées du chantier de notre gnomoniste correspondent à un lieu situé en France, ce qui nous permet de connaître la relation entre l’heure légale et le temps universel et ainsi extraire précisément les déclinaisons des éphémérides. Si, d’un côté, nous connaissons exactement l’heure légale de \(t_1\), l’heure approximative de \(t_2\), « à la première heure », nous suffira pour obtenir la valeur de \(d_2\) avec une précision suffisante en prenant par exemple \(7\) h. Notons au passage que notre énigme se situe en 2010 et que, depuis 1976 en France, un changement d’heure est appliqué en été. Il s’effectue le dernier weekend de mars, donc entre \(t_1\) et \(t_2\). En prenant toutes ces données en compte nous obtenons à partir des éphémérides :
\(d_1 = -0,91°\) d’où \(NS_1 = 90,91°\)
\(d_2 = 7,16°\) d’où \(NS_2 = 82,84°\)
Les 3 points \(S_1\), \(S_2\) et \(N\) forment un triangle sphérique dont nous connaissons maintenant les 3 côtés et nous pouvons calculer l’angle en \(N\) qui représente la différence des heures solaires aux instants \(t_1\) et \(t_2\). TriSph nous donne cet angle directement en heure : \(N = 3\) h \(58\) min \(49\) s

Pour passer de l’heure légale \(hl_1\) et \(hl_2\) à l’heure solaire aux instants \(t_1\) et \(t_2\) nous avons besoin des équations du temps \(et_1\) et \(et_2\). Comme pour la déclinaison, \(et_1\) s’obtient précisément sachant que \(t_1\) est parfaitement défini et \(et_2\) peut s’obtenir avec une précision suffisante en partant d’une valeur approchée de \(t_2\). En prenant \(7\) h pour l’heure légale de \(t_2\), les éphémérides nous donnent :
\(et_1 = 8\) min \(6\) s
\(et_2 = 1\) min \(57\) s
Sachant enfin que notre gnomoniste retourne sur son chantier plus tôt qu’il l’a quitté et en appelant \(cl\) la correction de longitude, nous pouvons écrire :
\((hl_1 – et_1 – cl – 1\) h\() – (hl_2 – et_2 – cl – 2\) h\() = N\)
d’où \(hl_2 = hl_1 – et_1 + et_2 + 1\) h \(– N\)
\(hl_2 = 11\):\(12\):\(00 - 00\):\(08\):\(06 + 00\):\(01\):\(57 + 1\):\(00\):\(00 - 3\):\(58\):\(49 = 8\):\(07\):\(02\)
Au retour de notre gnomoniste sur son chantier, sa montre indique donc \(8\) h \(7\) min
Remarquons que, curieusement, nous avons obtenu ce résultat sans utiliser les valeurs numériques de la position géographique ni avoir recours à l’orientation de la planchette, ces grandeurs étant généralement jugées indispensables en gnomonique. Cet apriori nous conduirait, dans ce cas, à des équations inextricables.
Si, comme l’a supposé Stéphane, la montre du gnomoniste avait été réglée sur l’heure solaire, les déclinaisons obtenues ci-dessus peuvent toujours être considérées comme justes ainsi que le calcul qui les utilise, l’angle en \(N\). Il n’y a donc à reconsidérer que le dernier calcul qui s’écrit alors plus simplement :
\(hs_2 = hs_1 – N = 11\):\(12\):\(00 - 3\):\(58\):\(49 = 7\):\(13\):\(11\)
Yvon Massé - Site perso. : La gnomonique
Re: Énigme : la planchette du gnomoniste
Bonjour à tous,
Merci Yvon pour cette belle démonstration. C'est très clair
Je n'avais pas pensé à raisonner de cette façon. Ce qui me posait problème c'était le manque d'information sur le choix du repère
J'ai essayé 3 méthodes:
1) trigonométrie sphérique et plane
2) En fixant un repère j'ai aussi essayé d'utiliser la méthode des 2 points d'ombre.
3) résolution de l'équation sinh = sin(phi)sin(delta)+cos(phi)cos(delta)cos(H) puisqu'il fallait prendre de la hauteur .......
En tout cas merci pour ce joli problème.
Yvon n'hésite pas à en proposer d'autres ....
Bon dimanche
seb
Merci Yvon pour cette belle démonstration. C'est très clair
Je n'avais pas pensé à raisonner de cette façon. Ce qui me posait problème c'était le manque d'information sur le choix du repère
J'ai essayé 3 méthodes:
1) trigonométrie sphérique et plane
2) En fixant un repère j'ai aussi essayé d'utiliser la méthode des 2 points d'ombre.
3) résolution de l'équation sinh = sin(phi)sin(delta)+cos(phi)cos(delta)cos(H) puisqu'il fallait prendre de la hauteur .......
En tout cas merci pour ce joli problème.
Yvon n'hésite pas à en proposer d'autres ....
Bon dimanche
seb