Cadran des Balkans
- Yvon_M
- Administrateur du site
- Messages : 412
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Cadran des Balkans
Encore un beau programme Stéphane !
Il permet de vulgariser cet astucieux cadran que je ne connaissais pas encore et qui montre, si c’était encore nécessaire, l’immense ingéniosité des anciens.
Comme d’habitude, j’ai rajouté le lien dans le message Les programmes GeoGebra de Stéphane
Il permet de vulgariser cet astucieux cadran que je ne connaissais pas encore et qui montre, si c’était encore nécessaire, l’immense ingéniosité des anciens.
Comme d’habitude, j’ai rajouté le lien dans le message Les programmes GeoGebra de Stéphane
Yvon Massé - Site perso. : La gnomonique
- Yvon_M
- Administrateur du site
- Messages : 412
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Cadran des Balkans
J’ai eu l’occasion de me pencher récemment sur cette merveille d’ingéniosité et je vous propose d’expliquer son fonctionnement par la géométrie, ce qui permettra de bien visualiser l’approximation effectuée et, peut-être, de se donner une idée sur la façon dont on a pu imaginer ce cadran, en effet les outils que nous utiliserons sont ceux que maîtrisaient parfaitement ses concepteurs.
Dans cette première contribution, je donnerai d’abord quelques éléments afin de bien situer ce cadran pour lequel on trouve de nombreux écrits mais qui, malheureusement, peuvent apporter une grande confusion.
Le cadran des Balkans fait partie d’une famille dont une bonne dizaine d’exemplaires ont été retrouvés et dont on situe la fabrication entre le Ier et le VIe s. apr. J.-C. Le premier a été découverts entre 1730 et 1740 près de Rome et le second une centaine d’années plus tard en France, dans le département de la Loire à Crêt-Chatelard. Tous les deux avaient le porte-ombre cassé et sont actuellement perdus. Les érudits qui ont décrit ces cadrans n’ont pas compris comment les utiliser (1). Ce n’est qu’en 1925, dans son livre Die Theorie der Sonnenuhren, que J. Drecker a proposé un mode d’utilisation cohérent qui utilise la totalité des inscriptions de l’instrument et qui permet de relever les heures inégales avec une approximation parfaitement acceptable. C’est le mode d’emploi qui est donné dans l’article de D. Savoie (2) mentionné par Stéphane et qui est utilisé dans son programme.
La majorité des exemplaires retrouvés ne sont pas complets. Parmi les rares qui le sont (au moins 2), il y a celui du Musée d’histoire des sciences d’Oxford (celui qui apparaît dans le programme de Stéphane) et dont on peut voir de magnifiques photos ici :
https://www.hsm.ox.ac.uk/collections-on ... rative-307
En voici une qui présente les différentes pièces démontées afin de mieux comprendre leurs fonctions.

A : platine principale avec, en haut, l’anneau de suspension et, sur la droite, l’échelle des latitudes de 30 à 60°.
B : plaque venant s’insérer dans la platine en plaçant son index, en haut à droite, en face de l’échelle des latitudes. Elle comporte deux échelles des signes symétriques.
C : porte ombre et sa clavette pour rassembler les pièces, à régler sur le signe du jour d’observation. Les graduations horaires sont gravées sur la surface incurvée.
Sur les photos suivantes, à gauche on peut voir la face arrière de la platine qui reçoit une liste de lieux avec la latitude correspondante. À droite, le cadran est remonté et prêt à être utilisé pour une latitude d’environ 46° à une date situé à une dizaine de jours avant l’équinoxe de printemps, ou après celui d’automne.

Sur l’illustration suivante (3), qui représente une reconstitution de l’exemplaire conservé au British Museum et qu’on peut admirer ici :
https://www.britishmuseum.org/collectio ... 997-0303-1
on peut voir un système de suspension différent mais le principe du cadran reste identique.
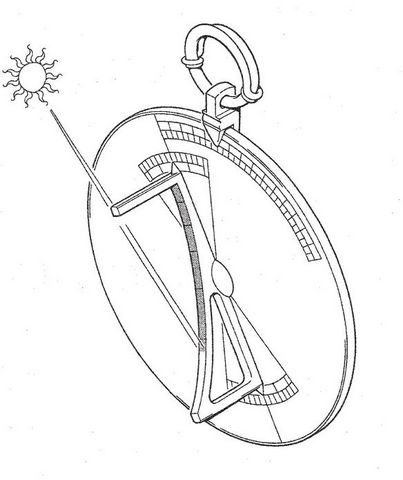
L’utilisation consiste à suspendre le cadran et à l’orienter de façon que l’ombre du gnomon s’aligne parfaitement avec la surface incurvée et à lire l’heure indiquée. Le réglage du cadran reste inchangé toute la journée, en effet il est toujours possible de faire porter l’ombre correctement en orientant le cadran, même si le Soleil est passé à l’ouest.
Ce mode d’utilisation est très spécifique et il est difficile de le rapprocher de celui d’un autre type de cadran solaire, ce qui explique peut-être le temps qu’il a fallu pour le retrouver. Son classement aussi ne tombe pas sous le sens : ce n’est pas un cadran d’angle horaire ni un cadran d’azimut, c’est donc un cadran de hauteur, ce qui apparaîtra plus clairement dans le message suivant.
Terminons enfin avec le nom que l’on peut lui donner. Au livre IX de son De Architectura, Vitruve énumère des cadrans en les associant à leur inventeur : le « pros pan klima » (littéralement « pour toutes les latitudes » en grec) est attribué à Theodosius et Andreas sans aucune autre précision. À la fin du XVIIIe siècle, Montucla est peut-être le premier à faire le rapprochement entre ce passage et le cadran trouvé près de Rome (4). Depuis, il s’avère que parmi tous les cadrans retrouvés datant de l’Antiquité, les seuls qui ont la possibilité de fonctionner pour différentes latitudes sont tous de ce modèle, de là à les dénommer « pros pan klima » il n’y a qu’un pas que beaucoup ont franchi, mais les historiens des sciences préfèrent rester sur la réserve et parlent de « cadran portable romain universel ».
À bientôt pour aborder géométriquement les aspects techniques...
(1) ^ Baldani en 1741 et Durand/de la Noë en 1897. Voir respectivement :
https://books.google.fr/books?id=oMtNz-YSnkUC&pg=PA185
https://gallica.bnf.fr/ark:/12148/bpt6k408247n/f5
(2) ^ D. Savoie a complété cet article pour en faire l’objet du chapitre II de son livre Recherches sur les cadrans solaire, Brépols, 2014. Une traduction en anglais de ce chapitre se retrouve dans une publication plus récente de D. Savoie, Three examples of ancient “universal” portable sundials, 2020, téléchargeable ici :
https://archive.nyu.edu/bitstream/2451/ ... Savoie.pdf
(3) ^ Crédit : Ackermann 2003 / Light on Byzantium: A Universal Sundial in the British Museum
(4) ^ Histoire des Mathématiques, tome 1, 1799 - Supplément contenant l’histoire de la gnomonique, p. 724
Dans cette première contribution, je donnerai d’abord quelques éléments afin de bien situer ce cadran pour lequel on trouve de nombreux écrits mais qui, malheureusement, peuvent apporter une grande confusion.
Le cadran des Balkans fait partie d’une famille dont une bonne dizaine d’exemplaires ont été retrouvés et dont on situe la fabrication entre le Ier et le VIe s. apr. J.-C. Le premier a été découverts entre 1730 et 1740 près de Rome et le second une centaine d’années plus tard en France, dans le département de la Loire à Crêt-Chatelard. Tous les deux avaient le porte-ombre cassé et sont actuellement perdus. Les érudits qui ont décrit ces cadrans n’ont pas compris comment les utiliser (1). Ce n’est qu’en 1925, dans son livre Die Theorie der Sonnenuhren, que J. Drecker a proposé un mode d’utilisation cohérent qui utilise la totalité des inscriptions de l’instrument et qui permet de relever les heures inégales avec une approximation parfaitement acceptable. C’est le mode d’emploi qui est donné dans l’article de D. Savoie (2) mentionné par Stéphane et qui est utilisé dans son programme.
La majorité des exemplaires retrouvés ne sont pas complets. Parmi les rares qui le sont (au moins 2), il y a celui du Musée d’histoire des sciences d’Oxford (celui qui apparaît dans le programme de Stéphane) et dont on peut voir de magnifiques photos ici :
https://www.hsm.ox.ac.uk/collections-on ... rative-307
En voici une qui présente les différentes pièces démontées afin de mieux comprendre leurs fonctions.

A : platine principale avec, en haut, l’anneau de suspension et, sur la droite, l’échelle des latitudes de 30 à 60°.
B : plaque venant s’insérer dans la platine en plaçant son index, en haut à droite, en face de l’échelle des latitudes. Elle comporte deux échelles des signes symétriques.
C : porte ombre et sa clavette pour rassembler les pièces, à régler sur le signe du jour d’observation. Les graduations horaires sont gravées sur la surface incurvée.
Sur les photos suivantes, à gauche on peut voir la face arrière de la platine qui reçoit une liste de lieux avec la latitude correspondante. À droite, le cadran est remonté et prêt à être utilisé pour une latitude d’environ 46° à une date situé à une dizaine de jours avant l’équinoxe de printemps, ou après celui d’automne.

Sur l’illustration suivante (3), qui représente une reconstitution de l’exemplaire conservé au British Museum et qu’on peut admirer ici :
https://www.britishmuseum.org/collectio ... 997-0303-1
on peut voir un système de suspension différent mais le principe du cadran reste identique.

L’utilisation consiste à suspendre le cadran et à l’orienter de façon que l’ombre du gnomon s’aligne parfaitement avec la surface incurvée et à lire l’heure indiquée. Le réglage du cadran reste inchangé toute la journée, en effet il est toujours possible de faire porter l’ombre correctement en orientant le cadran, même si le Soleil est passé à l’ouest.
Ce mode d’utilisation est très spécifique et il est difficile de le rapprocher de celui d’un autre type de cadran solaire, ce qui explique peut-être le temps qu’il a fallu pour le retrouver. Son classement aussi ne tombe pas sous le sens : ce n’est pas un cadran d’angle horaire ni un cadran d’azimut, c’est donc un cadran de hauteur, ce qui apparaîtra plus clairement dans le message suivant.
Terminons enfin avec le nom que l’on peut lui donner. Au livre IX de son De Architectura, Vitruve énumère des cadrans en les associant à leur inventeur : le « pros pan klima » (littéralement « pour toutes les latitudes » en grec) est attribué à Theodosius et Andreas sans aucune autre précision. À la fin du XVIIIe siècle, Montucla est peut-être le premier à faire le rapprochement entre ce passage et le cadran trouvé près de Rome (4). Depuis, il s’avère que parmi tous les cadrans retrouvés datant de l’Antiquité, les seuls qui ont la possibilité de fonctionner pour différentes latitudes sont tous de ce modèle, de là à les dénommer « pros pan klima » il n’y a qu’un pas que beaucoup ont franchi, mais les historiens des sciences préfèrent rester sur la réserve et parlent de « cadran portable romain universel ».
À bientôt pour aborder géométriquement les aspects techniques...
(1) ^ Baldani en 1741 et Durand/de la Noë en 1897. Voir respectivement :
https://books.google.fr/books?id=oMtNz-YSnkUC&pg=PA185
https://gallica.bnf.fr/ark:/12148/bpt6k408247n/f5
(2) ^ D. Savoie a complété cet article pour en faire l’objet du chapitre II de son livre Recherches sur les cadrans solaire, Brépols, 2014. Une traduction en anglais de ce chapitre se retrouve dans une publication plus récente de D. Savoie, Three examples of ancient “universal” portable sundials, 2020, téléchargeable ici :
https://archive.nyu.edu/bitstream/2451/ ... Savoie.pdf
(3) ^ Crédit : Ackermann 2003 / Light on Byzantium: A Universal Sundial in the British Museum
(4) ^ Histoire des Mathématiques, tome 1, 1799 - Supplément contenant l’histoire de la gnomonique, p. 724
Yvon Massé - Site perso. : La gnomonique
Re: Cadran des Balkans
Bonjour,
Merci pour ce partage très intéressant
Merci Stéphane pour cette remarquable animation très pédagogique et merci à Yvon pour ces rappels historiques.
Je m'étais également penché sur l'aspect théorique de ce cadran et certains points me paraissaient obscurs !
Du coup j'ai hâte de lire la démonstration géométrique d'Yvon.
A bientôt
SebB
Merci pour ce partage très intéressant
Merci Stéphane pour cette remarquable animation très pédagogique et merci à Yvon pour ces rappels historiques.
Je m'étais également penché sur l'aspect théorique de ce cadran et certains points me paraissaient obscurs !
Du coup j'ai hâte de lire la démonstration géométrique d'Yvon.
A bientôt
SebB
- Yvon_M
- Administrateur du site
- Messages : 412
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Cadran des Balkans
Voici donc la suite de la première partie avec, avant toute chose, une référence que j’ai trouvée entre-temps et qui a le mérite de répertorier tous les cadrans portables romains, universels ou non, avec une carte des lieux où ils ont été retrouvés :
https://shs.cairn.info/revue-du-nord-2012-5-page-97
Abordons maintenant la justification du fonctionnement du cadran universel par la géométrie. Cette approche a déjà fait l’objet de deux publications dont on peut trouver la première, de F. Stebbins en 1958, ici :
https://articles.adsabs.harvard.edu/pdf ... ..52..250S
Bien qu’elle ne s’appuie pas sur un développement rigoureux, elle a le mérite de mettre en place une configuration initiale cohérente et de fournir, en conclusion, une figure donnant une idée correcte de l’approximation obtenue. La seconde publication (5), qui n’est malheureusement pas en accès libre sur Internet, reprend la configuration de la première et, après deux rabattements, utilise la trigonométrie plane pour obtenir l’expression de l’approximation. Ce que je vous présenterai ici est la reprise de la partie géométrique de cette seconde publication avec un complément permettant de retrouver la figure en conclusion de la publication de Stebbins et, de façon plus simple, l’expression de l’approximation.
La figure suivante représente une perspective de la sphère céleste au dessus de l’horizon NESW pour une latitude positive. L’observateur se trouve en O, centre de la sphère céleste. Le méridien est représenté par le demi-cercle SMPN, P étant le pôle Nord. La déclinaison du Soleil est positive et sa course correspond à la portion de cercle LAML’. Elle est centrée sur le point C qui se trouve sur l’axe polaire OP. L’Angle Ho est le demi-angle diurne. Enfin, considérons que le Soleil se trouve en A, son angle horaire est H ou encore l’angle de l’arc MA.
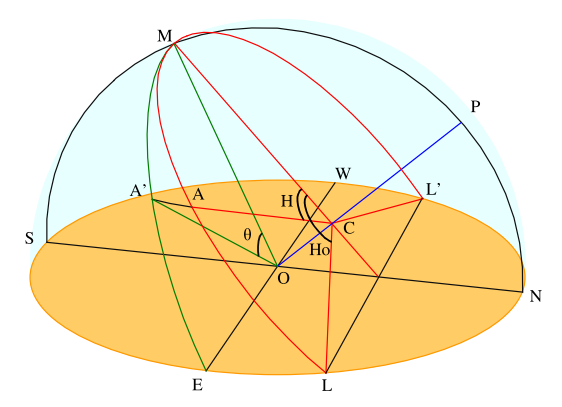
Fig. 1 : la sphère céleste en perspective
Intéressons-nous maintenant à la mesure du cadran romain en sachant que son réglage est tel que, quand il est suspendu et que le disque du cadran est dans le plan du méridien, l’axe du porte-ombre amovible est dirigé vers la position du Soleil à midi vrai, ainsi le quart de plan défini par le porte-ombre et son échelle de mesure dessine sur la sphère un quart de grand cercle, représenté en vert sur la figure, qui passe par les points M et E. Suivant le mode d’utilisation du cadran, il faut que le Soleil soit situé dans ce quart de plan, ce qui s’obtient en faisant tourner le cadran autour de l’axe vertical. Dans le cadre de notre figure, ce qui reviendra au même, c’est le Soleil que nous allons reporter de A en A’, par rotation autours de l’axe vertical. La mesure, qui consiste à évaluer la position de A’ sur le quart de cercle EM, utilise donc la hauteur du Soleil sur l’horizon d’où la classification indiquée dans la première partie. Par similitude avec l’angle horaire H et par commodité pour l’évaluation finale, la position A’ sera repérée par l’angle de l’arc MA’, ou encore l’angle θ.
Plaçons-nous, figure suivante, dans le plan du méridien et intéressons-nous à la projection orthogonale des éléments de la sphère sur ce plan, c’est-a-dire utilisons la technique ancienne connue sous le nom d’analemme (6).
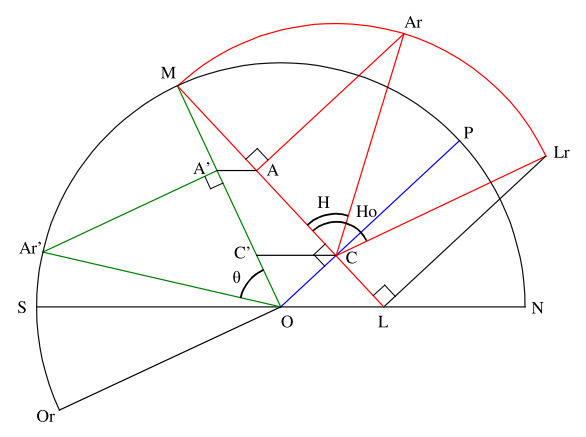
Fig. 2 : projection de la sphère céleste sur le méridien et rabattements
On retrouve le demi-cercle SMPN du méridien et le diamètre SN passant par le centre O. Le segment ML est la trace de la course diurne du Soleil, elle est perpendiculaire à l’axe polaire OP. Pour trouver la position A du Soleil sur cette trace, rabattons autours de celle-ci la portion de cercle MAL de la figure 1. On peut tracer facilement ce rabattement en tirant du centre C un cercle passant par M puis en traçant les rayons CAr et CLr faisant respectivement les angles H et Ho avec CM. De Ar, il suffit de descendre une perpendiculaire à ML pour obtenir le point A.
Le rayon OM est la trace du quart de plan correspondant au porte-ombre amovible. Pour trouver l’angle mesuré nous allons rabattre la portion de cercle MA’E de la figure 1 autour de OM pour obtenir le quart de cercle MSOr qui se confond en partie avec le demi-cercle du méridien. À présent, pour obtenir l’angle θ mesuré, il suffit de reporter A sur le rayon OM en traçant une parallèle à SN et, du point A’ obtenu, tirer une perpendiculaire à OM pour obtenir le point Ar’, l’angle θ est la mesure de l’arc MAr’.
Cette figure a l’avantage de représenter sur un même plan, d’un côté en rouge, la course du Soleil et de l’autre, en vert, la mesure effectuée par le cadran. Pour que le comparaison soit encore plus facile, remarquons que les angles H et Ho sont entièrement définis par les rapports respectifs de CA et CL à CM (qui correspondent en terme moderne aux cosinus de H et Ho). Si nous reportons le point C en C’ par une ligne parallèle à SN, d’après le théorème de Thalès, nous retrouvons les mêmes rapports avec C’A’, C’O et C’M. En d’autres termes, nous pouvons compresser et déplacer la partie rouge de la figure pour venir « coller » le segment ML sur MO tout en conservant les angles H et Ho. On obtient ainsi la figure 3 suivante qui a l’avantage supplémentaire d’être plus simple.
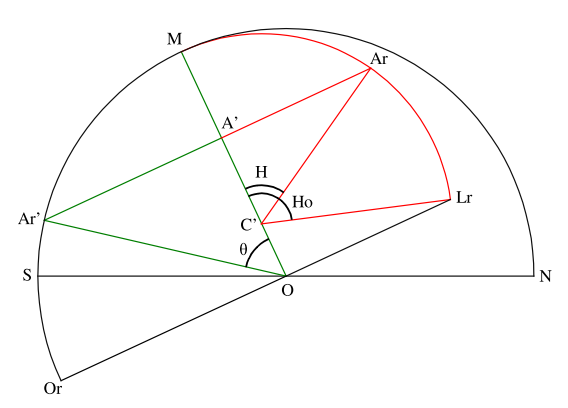
Fig. 3 : relation entre θ, H et Ho pour une déclinaison positive
Le même exercice avec une déclinaison du Soleil négative, en inversant les parties rouge et verte, donne la figure 4 suivante. Dans celle-ci la partie rouge a été dilatée.
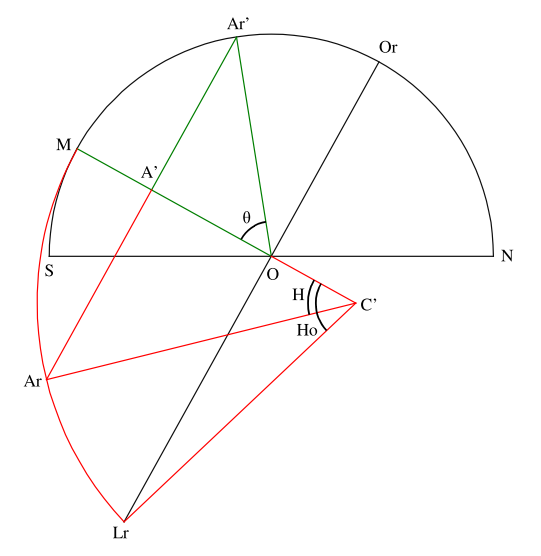
Fig. 4 : relation entre θ, H et Ho pour une déclinaison négative
On comprendra facilement que si la déclinaison est nulle, les points O, C et L de la figure 2 sont confondus. Il s’en suit que Ho = 90°, les parties rouge et verte sont identiques et que θ = H.
Rassemblons à la figure 5 les différents arcs semi-diurnes des déclinaisons positive, négative et nulle du Soleil.
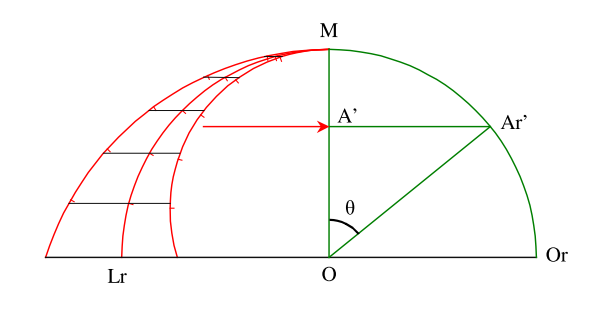
Fig. 5 : compromis de la graduation de θ pour toutes les déclinaisons
Le principe des heures inégales est de découper la journée en 12 durées égales ou, ce qui revient au même, la course semi-diurne du Soleil en 6 parties égales. Ces divisions ont été tracées à la figure 5 et elles font apparaître qu’un compromis intéressant pour la graduation de l’échelle de mesure de θ est la division du quart de cercle MAr’Or en 6 partie égales de 15°, ce qui permet notamment d’avoir une erreur nulle aux équinoxes.
Comme indiqué dans l’introduction de ce message, on retrouve en conclusion de la publication de F. Stebbins la figure suivante qui est similaire à la figure 5, mais organisée différemment.
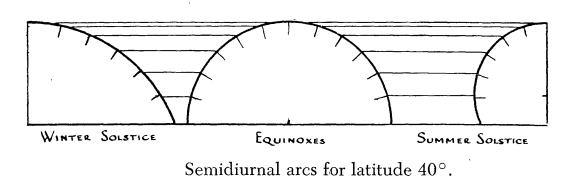
La figure 5 apparaît aussi sous une autre forme dans le postulat de l’approximation qui a permis de trouver la géométrie d’un cadran à lignes horaires parallèles puis celle du quadrant ancien dans ce sujet :
viewtopic.php?t=121
Il est effectivement assez curieux de remarquer que le cadran romain universel et le quadrant ancien, qui sont de forme et d’utilisation entièrement différentes, reposent rigoureusement sur la même base d’approximation.
Je vous laisse le temps de bien comprendre ce que je vous ai présenté et, éventuellement, me poser des questions si certains points n’étaient pas suffisamment clairs avant d’aborder dans une prochaine partie les aspects trigonométriques qui permettront de quantifier l’approximation.
(5) ^ M. T. Wright : Greek and Roman Portable Sundials. An Ancient Essay in Approximation, 2000. Dans Archive for History of Exact Sciences, t. 55, p. 177-187
(6) ^ Voir De l’Analemme aux cadrans de hauteur, Y. Massé, 2009 disponible ici :
https://shs.cairn.info/revue-du-nord-2012-5-page-97
Abordons maintenant la justification du fonctionnement du cadran universel par la géométrie. Cette approche a déjà fait l’objet de deux publications dont on peut trouver la première, de F. Stebbins en 1958, ici :
https://articles.adsabs.harvard.edu/pdf ... ..52..250S
Bien qu’elle ne s’appuie pas sur un développement rigoureux, elle a le mérite de mettre en place une configuration initiale cohérente et de fournir, en conclusion, une figure donnant une idée correcte de l’approximation obtenue. La seconde publication (5), qui n’est malheureusement pas en accès libre sur Internet, reprend la configuration de la première et, après deux rabattements, utilise la trigonométrie plane pour obtenir l’expression de l’approximation. Ce que je vous présenterai ici est la reprise de la partie géométrique de cette seconde publication avec un complément permettant de retrouver la figure en conclusion de la publication de Stebbins et, de façon plus simple, l’expression de l’approximation.
La figure suivante représente une perspective de la sphère céleste au dessus de l’horizon NESW pour une latitude positive. L’observateur se trouve en O, centre de la sphère céleste. Le méridien est représenté par le demi-cercle SMPN, P étant le pôle Nord. La déclinaison du Soleil est positive et sa course correspond à la portion de cercle LAML’. Elle est centrée sur le point C qui se trouve sur l’axe polaire OP. L’Angle Ho est le demi-angle diurne. Enfin, considérons que le Soleil se trouve en A, son angle horaire est H ou encore l’angle de l’arc MA.

Fig. 1 : la sphère céleste en perspective
Intéressons-nous maintenant à la mesure du cadran romain en sachant que son réglage est tel que, quand il est suspendu et que le disque du cadran est dans le plan du méridien, l’axe du porte-ombre amovible est dirigé vers la position du Soleil à midi vrai, ainsi le quart de plan défini par le porte-ombre et son échelle de mesure dessine sur la sphère un quart de grand cercle, représenté en vert sur la figure, qui passe par les points M et E. Suivant le mode d’utilisation du cadran, il faut que le Soleil soit situé dans ce quart de plan, ce qui s’obtient en faisant tourner le cadran autour de l’axe vertical. Dans le cadre de notre figure, ce qui reviendra au même, c’est le Soleil que nous allons reporter de A en A’, par rotation autours de l’axe vertical. La mesure, qui consiste à évaluer la position de A’ sur le quart de cercle EM, utilise donc la hauteur du Soleil sur l’horizon d’où la classification indiquée dans la première partie. Par similitude avec l’angle horaire H et par commodité pour l’évaluation finale, la position A’ sera repérée par l’angle de l’arc MA’, ou encore l’angle θ.
Plaçons-nous, figure suivante, dans le plan du méridien et intéressons-nous à la projection orthogonale des éléments de la sphère sur ce plan, c’est-a-dire utilisons la technique ancienne connue sous le nom d’analemme (6).

Fig. 2 : projection de la sphère céleste sur le méridien et rabattements
On retrouve le demi-cercle SMPN du méridien et le diamètre SN passant par le centre O. Le segment ML est la trace de la course diurne du Soleil, elle est perpendiculaire à l’axe polaire OP. Pour trouver la position A du Soleil sur cette trace, rabattons autours de celle-ci la portion de cercle MAL de la figure 1. On peut tracer facilement ce rabattement en tirant du centre C un cercle passant par M puis en traçant les rayons CAr et CLr faisant respectivement les angles H et Ho avec CM. De Ar, il suffit de descendre une perpendiculaire à ML pour obtenir le point A.
Le rayon OM est la trace du quart de plan correspondant au porte-ombre amovible. Pour trouver l’angle mesuré nous allons rabattre la portion de cercle MA’E de la figure 1 autour de OM pour obtenir le quart de cercle MSOr qui se confond en partie avec le demi-cercle du méridien. À présent, pour obtenir l’angle θ mesuré, il suffit de reporter A sur le rayon OM en traçant une parallèle à SN et, du point A’ obtenu, tirer une perpendiculaire à OM pour obtenir le point Ar’, l’angle θ est la mesure de l’arc MAr’.
Cette figure a l’avantage de représenter sur un même plan, d’un côté en rouge, la course du Soleil et de l’autre, en vert, la mesure effectuée par le cadran. Pour que le comparaison soit encore plus facile, remarquons que les angles H et Ho sont entièrement définis par les rapports respectifs de CA et CL à CM (qui correspondent en terme moderne aux cosinus de H et Ho). Si nous reportons le point C en C’ par une ligne parallèle à SN, d’après le théorème de Thalès, nous retrouvons les mêmes rapports avec C’A’, C’O et C’M. En d’autres termes, nous pouvons compresser et déplacer la partie rouge de la figure pour venir « coller » le segment ML sur MO tout en conservant les angles H et Ho. On obtient ainsi la figure 3 suivante qui a l’avantage supplémentaire d’être plus simple.

Fig. 3 : relation entre θ, H et Ho pour une déclinaison positive
Le même exercice avec une déclinaison du Soleil négative, en inversant les parties rouge et verte, donne la figure 4 suivante. Dans celle-ci la partie rouge a été dilatée.

Fig. 4 : relation entre θ, H et Ho pour une déclinaison négative
On comprendra facilement que si la déclinaison est nulle, les points O, C et L de la figure 2 sont confondus. Il s’en suit que Ho = 90°, les parties rouge et verte sont identiques et que θ = H.
Rassemblons à la figure 5 les différents arcs semi-diurnes des déclinaisons positive, négative et nulle du Soleil.

Fig. 5 : compromis de la graduation de θ pour toutes les déclinaisons
Le principe des heures inégales est de découper la journée en 12 durées égales ou, ce qui revient au même, la course semi-diurne du Soleil en 6 parties égales. Ces divisions ont été tracées à la figure 5 et elles font apparaître qu’un compromis intéressant pour la graduation de l’échelle de mesure de θ est la division du quart de cercle MAr’Or en 6 partie égales de 15°, ce qui permet notamment d’avoir une erreur nulle aux équinoxes.
Comme indiqué dans l’introduction de ce message, on retrouve en conclusion de la publication de F. Stebbins la figure suivante qui est similaire à la figure 5, mais organisée différemment.

La figure 5 apparaît aussi sous une autre forme dans le postulat de l’approximation qui a permis de trouver la géométrie d’un cadran à lignes horaires parallèles puis celle du quadrant ancien dans ce sujet :
viewtopic.php?t=121
Il est effectivement assez curieux de remarquer que le cadran romain universel et le quadrant ancien, qui sont de forme et d’utilisation entièrement différentes, reposent rigoureusement sur la même base d’approximation.
Je vous laisse le temps de bien comprendre ce que je vous ai présenté et, éventuellement, me poser des questions si certains points n’étaient pas suffisamment clairs avant d’aborder dans une prochaine partie les aspects trigonométriques qui permettront de quantifier l’approximation.
(5) ^ M. T. Wright : Greek and Roman Portable Sundials. An Ancient Essay in Approximation, 2000. Dans Archive for History of Exact Sciences, t. 55, p. 177-187
(6) ^ Voir De l’Analemme aux cadrans de hauteur, Y. Massé, 2009 disponible ici :
Contenu réservé aux adhérents connectés.
Yvon Massé - Site perso. : La gnomonique
Re: Cadran des Balkans
Bonjour,
Merci Yvon pour ce beau travail.
J'ai lu attentivement et dès le départ je suis malheureusement bloqué par la compréhension de ce quart de cercle vert:
l’axe du porte-ombre amovible est dirigé vers la position du Soleil à midi vrai, ainsi le quart de plan défini par le porte-ombre et son échelle de mesure dessine sur la sphère un quart de grand cercle, représenté en vert sur la figure, qui passe par les points M et E. Suivant le mode d’utilisation du cadran, il faut que le Soleil soit situé dans ce quart de plan, ce qui s’obtient en faisant tourner le cadran autour de l’axe vertical
Je ne ne vois pas comment le porte ombre dessine le quart de cercle vert ?
Merci
Merci Yvon pour ce beau travail.
J'ai lu attentivement et dès le départ je suis malheureusement bloqué par la compréhension de ce quart de cercle vert:
l’axe du porte-ombre amovible est dirigé vers la position du Soleil à midi vrai, ainsi le quart de plan défini par le porte-ombre et son échelle de mesure dessine sur la sphère un quart de grand cercle, représenté en vert sur la figure, qui passe par les points M et E. Suivant le mode d’utilisation du cadran, il faut que le Soleil soit situé dans ce quart de plan, ce qui s’obtient en faisant tourner le cadran autour de l’axe vertical
Je ne ne vois pas comment le porte ombre dessine le quart de cercle vert ?
Merci
Re: Cadran des Balkans
C'est bon, je viens de comprendre en utilisant l'animation de Stéphane 
Re: Cadran des Balkans
Merci Yvon pour ce travail d'explication par l'analemme.
C'est très clair
C'est très clair
- Yvon_M
- Administrateur du site
- Messages : 412
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Cadran des Balkans
Pour cette troisième partie, avant d’aborder les relations trigonométriques permettant de quantifier l’erreur de principe de ce cadran universel, ce qui ne sera qu’une simple formalité, nous allons faire une petite vérification de principe sur sa géométrie. En effet, nous avons la chance de disposer d’excellentes photos de l’exemplaire du Musée d’histoire des sciences d’Oxford, ce qui permet d’effectuer des mesures angulaires avec une précision de l’ordre du degré. Alors ne boudons pas ce plaisir d’autant qu’il m’est arrivé, au sujet de la Navicula de Genève, de constater que ce type de vérification aurait évité à quelques commentateurs d’échafauder des théories sans objet.
Commençons par la platine principale en prenant comme ligne de référence celle qui est employée lors de son utilisation : la verticale. Ainsi l’angle que l’on doit trouver pour une latitude ϕ est son complément à 90°, soit 90°– ϕ.

Voici les résultats obtenus (toutes les valeurs indiquées dans les tableaux sont en degrés).
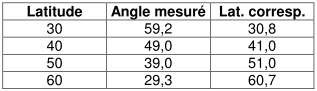
C’est pas mal et plutôt précis pour une pièce qui ne fait que 6 cm de diamètre.
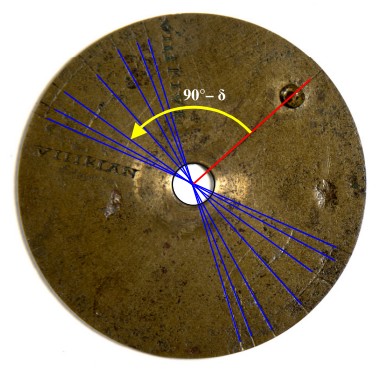
Voyons maintenant la plaque circulaire. Comme référence prenons le rayon qui passe par l’index, l’angle mesuré doit aussi, dans ce cas, être le complément à 90° de la déclinaison du Soleil. Rappelons que dans l’Antiquité on considérait que la déclinaison maximale était de 24°.
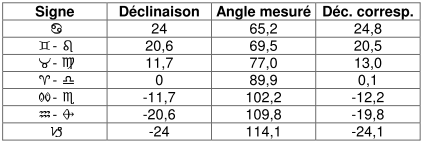
Jusque là tout va bien, on reste pratiquement dans le degré de différence.
Terminons par la mesure du porte-ombre avec son échelle horaire. C’est un peu plus sportif car celui-ci ne repose pas à plat sur le support de prise de vue à cause du renflement autours de son axe de rotation. En utilisant les autres vues, on peut toutefois estimer l’inclinaison à environ 12°. Il s’en suis un effet de perspective qui biaise légèrement la mesure. Dans les données exif du fichier image, par chance, la focale de l’optique (120 mm) et la référence de l’appareil photo (Nikon D800) sont indiquées. On peut ainsi connaître la taille du capteur (24x36 mm) et s’assurer que l’image n’a pas été détourée : elle contient effectivement tous les pixels du capteur. Avec le diamètre du cadran de 61 mm, il est ainsi possible de déterminer la champ de prise de vue (189x126 mm²) et la distance du centre optique : 631 mm, valeur cohérente avec un statif de prise de vue.
Ces informations sont suffisantes pour corriger la photo de la perspective - ce qui est fait sur les figures suivantes - pour ensuite effectuer les mesures angulaires. La référence utilisée est l’arête inférieure.

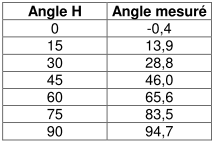
Aïe, ça pique un peu. On est loin des valeurs attendues pour les angles supérieurs à 45°…
Voyons si on peut imputer ces différences à une déformation du porte-ombre en procédant à l’envers : tirons depuis les encoches de l’échelle horaire des demi-droites faisant les angles 0°, 15°, 30°, etc. avec la droite de référence.

Là encore, le résultat n’est pas particulièrement probant, aucun point d’intersection commun ne semble se concrétiser. Le point de moindre erreur se situe toutefois un peu plus haut et plus à gauche que la position actuelle de l’arête utile du porte-ombre. Une légère amélioration serait donc obtenue en redressant le porte ombre perpendiculairement à la ligne de référence.
Dans tous les cas, si l’on veut rester sur l’hypothèse d’une graduation équi-angulaire, il faut accepter que les artisans qui ont réalisé cet objet ne sont pas parvenus à la même précision que pour les autres pièces, et cela sans raison apparente…
Terminons par le calcul de l’erreur de principe de ce cadran. Les heures inégales n sont comptées à partir du lever du Soleil, à ce moment là n = 0 hi. À midi vrai, n = 6 hi et n = 12 hi au coucher du Soleil. La relation entre H et n est :
H = n·Ho/6 – Ho
avec Ho = acos(–tan ϕ·tan δ), ainsi Ho est toujours positif et H a une valeur négative le matin et positive l’après-midi.
Établissons maintenant la relation entre la mesure θ et l’angle horaire H en se reportant à la figure 3 ou 4 de la seconde partie. En prenant pour unité le rayon C’Ar, nous avons :
OA’ = (1 – cos Ho)·cos θ = cos H – cos Ho
d’où :
cos θ = (cos H + tan ϕ·tan δ)/(1 + tan ϕ·tan δ)
Par convention, dans le but de simplifier la relation suivante, on peut prendre θ du même signe que H. Dans ce cas la mesure en heure inégale est :
m = θ/15 + 6
et l’erreur de principe, toujours en heure inégale :
e = m – n
Voici les courbes d’erreur que l’on peut tracer à partir de ces relations :
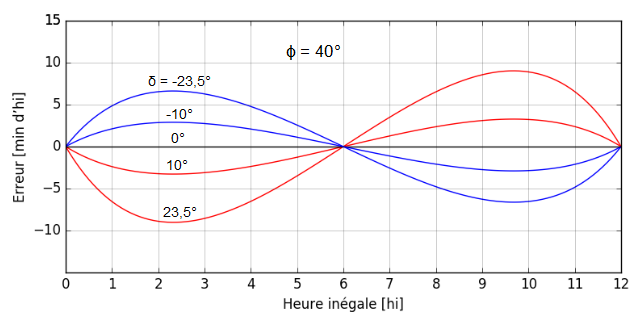
L’erreur augmente avec la déclinaison, elle est maximale vers 2 hi 20 et 9 hi 40. C’est au solstice d’été, à ces heures, que l’erreur est la plus importante.
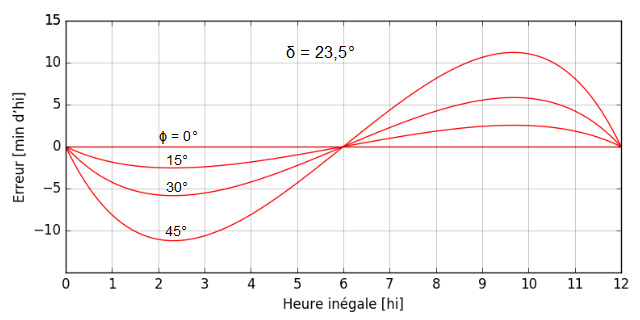
L’erreur augmente aussi avec la latitude. À 45°, elle ne dépasse pas 12 min d’heure inégale au solstice d’été.
D’après la similitude mentionnée à la fin de la seconde partie, ces relations et courbes sont aussi valables pour le quadrant ancien, et le cadran d’heures inégales à lignes parallèles dont on peut faire découler le quadrant.
Cette étude se termine ici et j’espère sincèrement qu’elle vous aura convaincu de la grande ingéniosité de nos anciens.
Commençons par la platine principale en prenant comme ligne de référence celle qui est employée lors de son utilisation : la verticale. Ainsi l’angle que l’on doit trouver pour une latitude ϕ est son complément à 90°, soit 90°– ϕ.

Voici les résultats obtenus (toutes les valeurs indiquées dans les tableaux sont en degrés).

C’est pas mal et plutôt précis pour une pièce qui ne fait que 6 cm de diamètre.
Voyons maintenant la plaque circulaire. Comme référence prenons le rayon qui passe par l’index, l’angle mesuré doit aussi, dans ce cas, être le complément à 90° de la déclinaison du Soleil. Rappelons que dans l’Antiquité on considérait que la déclinaison maximale était de 24°.


Jusque là tout va bien, on reste pratiquement dans le degré de différence.
Terminons par la mesure du porte-ombre avec son échelle horaire. C’est un peu plus sportif car celui-ci ne repose pas à plat sur le support de prise de vue à cause du renflement autours de son axe de rotation. En utilisant les autres vues, on peut toutefois estimer l’inclinaison à environ 12°. Il s’en suis un effet de perspective qui biaise légèrement la mesure. Dans les données exif du fichier image, par chance, la focale de l’optique (120 mm) et la référence de l’appareil photo (Nikon D800) sont indiquées. On peut ainsi connaître la taille du capteur (24x36 mm) et s’assurer que l’image n’a pas été détourée : elle contient effectivement tous les pixels du capteur. Avec le diamètre du cadran de 61 mm, il est ainsi possible de déterminer la champ de prise de vue (189x126 mm²) et la distance du centre optique : 631 mm, valeur cohérente avec un statif de prise de vue.
Ces informations sont suffisantes pour corriger la photo de la perspective - ce qui est fait sur les figures suivantes - pour ensuite effectuer les mesures angulaires. La référence utilisée est l’arête inférieure.


Aïe, ça pique un peu. On est loin des valeurs attendues pour les angles supérieurs à 45°…
Voyons si on peut imputer ces différences à une déformation du porte-ombre en procédant à l’envers : tirons depuis les encoches de l’échelle horaire des demi-droites faisant les angles 0°, 15°, 30°, etc. avec la droite de référence.

Là encore, le résultat n’est pas particulièrement probant, aucun point d’intersection commun ne semble se concrétiser. Le point de moindre erreur se situe toutefois un peu plus haut et plus à gauche que la position actuelle de l’arête utile du porte-ombre. Une légère amélioration serait donc obtenue en redressant le porte ombre perpendiculairement à la ligne de référence.
Dans tous les cas, si l’on veut rester sur l’hypothèse d’une graduation équi-angulaire, il faut accepter que les artisans qui ont réalisé cet objet ne sont pas parvenus à la même précision que pour les autres pièces, et cela sans raison apparente…
Terminons par le calcul de l’erreur de principe de ce cadran. Les heures inégales n sont comptées à partir du lever du Soleil, à ce moment là n = 0 hi. À midi vrai, n = 6 hi et n = 12 hi au coucher du Soleil. La relation entre H et n est :
H = n·Ho/6 – Ho
avec Ho = acos(–tan ϕ·tan δ), ainsi Ho est toujours positif et H a une valeur négative le matin et positive l’après-midi.
Établissons maintenant la relation entre la mesure θ et l’angle horaire H en se reportant à la figure 3 ou 4 de la seconde partie. En prenant pour unité le rayon C’Ar, nous avons :
OA’ = (1 – cos Ho)·cos θ = cos H – cos Ho
d’où :
cos θ = (cos H + tan ϕ·tan δ)/(1 + tan ϕ·tan δ)
Par convention, dans le but de simplifier la relation suivante, on peut prendre θ du même signe que H. Dans ce cas la mesure en heure inégale est :
m = θ/15 + 6
et l’erreur de principe, toujours en heure inégale :
e = m – n
Voici les courbes d’erreur que l’on peut tracer à partir de ces relations :

L’erreur augmente avec la déclinaison, elle est maximale vers 2 hi 20 et 9 hi 40. C’est au solstice d’été, à ces heures, que l’erreur est la plus importante.

L’erreur augmente aussi avec la latitude. À 45°, elle ne dépasse pas 12 min d’heure inégale au solstice d’été.
D’après la similitude mentionnée à la fin de la seconde partie, ces relations et courbes sont aussi valables pour le quadrant ancien, et le cadran d’heures inégales à lignes parallèles dont on peut faire découler le quadrant.
Cette étude se termine ici et j’espère sincèrement qu’elle vous aura convaincu de la grande ingéniosité de nos anciens.
Yvon Massé - Site perso. : La gnomonique
-
Stéphane_L
- Messages : 111
- Enregistré le : lun. 3 juin 2019 21:33
Re: Cadran des Balkans
Merci Yvon pour cette étude claire et passionante. Par sa rigueur et sa clarté, elle met en effet brillamment en lumière l'ingéniosité de nos anciens.