Ma réponse rapide de mercredi dernier n’est effectivement valable que pour un cas particulier : quand le Soleil et la réflexion son proche de l’équateur (plus rigoureusement, nous le verrons plus loin, quand les déclinaisons dR et dS sont opposées). J’ai naïvement cru que cette configuration se généralisait mais à l’évidence ce n’est pas le cas. Il y a notamment un contre exemple simple : quand on veut la réflexion suivant l’axe polaire. On comprend facilement que, dans ce cas, la vitesse angulaire du miroir doit être de 15°/h.
Pour analyser le problème de façon générale il faut donc prendre en compte la direction de la réflexion que l’on définira par une déclinaison dR et un angle horaire HR. De son côté, la direction du Soleil sera représentée par dS (déclinaison) et HS (angle horaire).
Pour simplifier les équations, on définira l’angle H = HS – HR ou, ce qui revient au même, on considérera comme origine des angles horaires le méridien contenant la direction de la réflexion. Les directions de la réflexion et du Soleil peuvent être représentées par des vecteurs unitaires, respectivement R et S. Pour déterminer la position à donner au miroir, on peut déterminer le vecteur normal à sa surface N qui s’exprime simplement par la somme vectorielle de R et S (N n’est pas unitaire). Ainsi nous avons en utilisant les coordonnées cartésiennes :
xR = cos(dR), yR = 0, zR = sin(dR)
xS = cos(H)*cos(dS), yS = -sin(H)*cos(dS), zS = sin(dS)
xN = cos(dR) + cos(H)*cos(dS), yN = -sin(H)*cos(dS), zN = sin(dR) + sin(dS)
Pour représenter la direction de N, on peut définir une déclinaison dN et un angle horaire HN tel que :
dN = asin(zN/racine(xN² + yN² + zN²))
HN = atan2(-yN, xN)
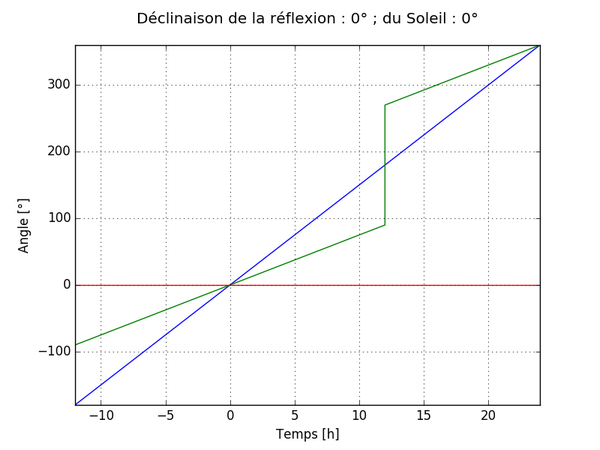
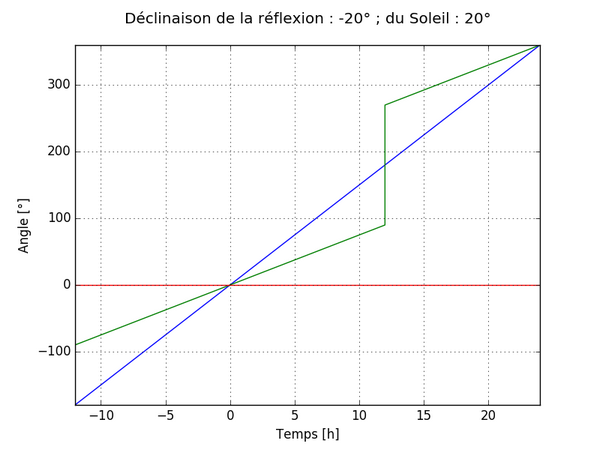
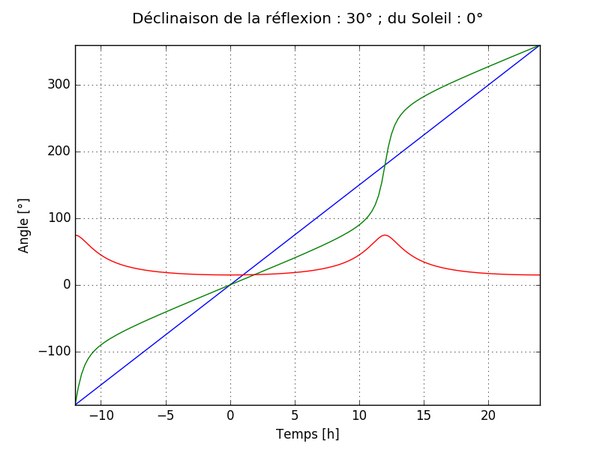
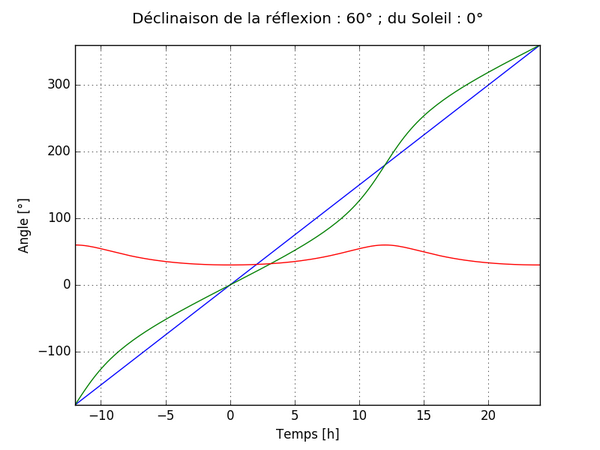
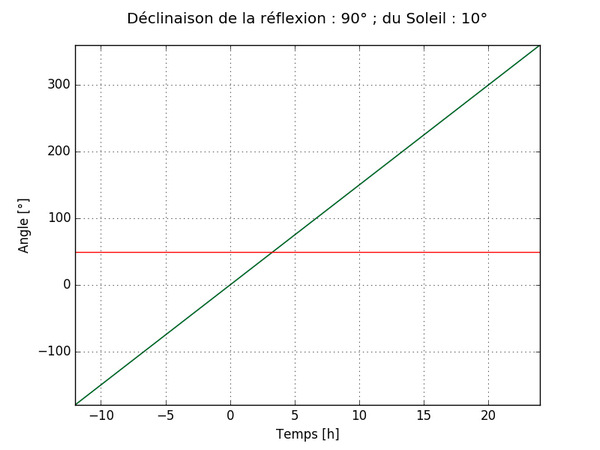
En représentant ensuite ces grandeurs sur un graphique avec le temps pour abscisse, on obtient les courbes suivantes en fonction des valeurs de dR et dS avec :
- En bleu l’angle H
- En vert l’angle HN
- En rouge l’angle dN