Page 1 sur 2
latitude équivalente
Posté : ven. 25 janv. 2019 11:11
par sebB
Bonjour,
je m'intéresse en ce moment à l'astrolabe universel.
j'ai lu le livre de Nicolas Bion intitulé " les usages de l'astrolabes tant universels que particuliers"
dans l'une de ses propositions, il propose de résoudre un problème d'astrologie sur les maisons Célestes avec un astrolabe universel.
le problème est le suivant: quelle est la longitude écliptique du commencement de chaque maison céleste?



En d'autres termes, c'est la longitude écliptique du point d'intersection entre chaque maison céleste et l'écliptique.
par exemple pour un endroit situé à la latitude de 49° et pour la maison céleste inclinée de 30° par rapport à l'horizon, il propose les étapes suivantes:
trouver l'endroit sur la terre où le plan incliné est horizontal, c'est à dire trouver la latitude équivalente. ceci correspond à un plan vertical déclinant tel que D=+90° et Z=30°.
trouver la longitude du point de l'écliptique qui se lève à cet endroit, c'est à dire l'ascendant. cette longitude sera la longitude recherchée.
comment se calcule la latitude équivalente?

A-t-on besoin de la longitude du lieu?
Merci
Re: latitude équivalente
Posté : ven. 25 janv. 2019 11:37
par sebB
Re: latitude équivalente
Posté : ven. 25 janv. 2019 21:07
par Yvon_M
Bonsoir sebB,
La latitude équivalente lae pour un cadran situé à la latitude la est donnée par la relation :
lae = asin(sin(la)*cos(Z) - cos(la)*cos(D)*sin(Z))
La longitude n’intervient pas, par contre le cadran horizontal équivalent (CHE) est situé à une certaine longitude loe dont la différence avec la longitude du cadran lo est :
loe - lo = atan2(cos(la)*cos(Z) + sin(la)*cos(D)*sin(Z), sin(D)*sin(Z))
avec atan2(1, racine(3)) = 60°
Pour trouver le lieu du CHE il « suffit » de se déplacer en ligne droite suivant la perpendiculaire au plan incliné et parcourir sur la terre une distance correspondant à l’angle de l’inclinaison. On peut donc obtenir ces relations par la résolution du triangle sphérique Pôle Nord – position du cadran – position du CHE.
En espérant que ces indications vous seront utiles dans vos recherches.
Re: latitude équivalente
Posté : ven. 25 janv. 2019 21:41
par Eric_M
Bonjour Seb.
Je suis content de voir que on travail sur les astrolabes universels avance !!
Si tu veux bien je vais essayer, non pas de répondre à ta question, Yvon l'a fait parfaitement, mais d'expliquer aux autres membres du forum le sens et les implications de ta question...
1) En astrologie traditionnelle (celle de la période médiévale), on pouvait distinguer deux démarches complémentaires: premièrement décrire l'état du ciel (position des étoiles et des planètes) à un moment particulier et ensuite en tirer des conclusions sur l'avenir, le destin etc... La première phase est un démarche scientifique tout à fait honorable, mais qui utilisait des concepts différents des notres. Notamment les planètes (au sens médiéval: Soleil, Lune etc..) étaient localisées dans des maisons.
2) Par définition, une maison est un "quartier" du ciel (1/12) limité par un arc joignant le point Nord et le point Sud de l'horizon local. C'est donc une division locale (liée à un lieu)
voir cette figure:
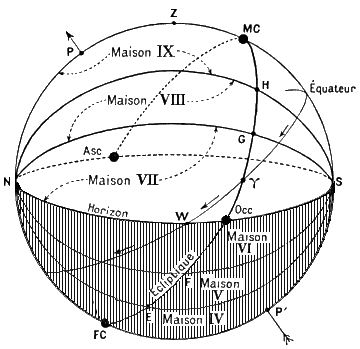
- fig06.gif (10.56 Kio) Vu 33316 fois
Les limites des maisons recoupent donc l'écliptique. Et ces points d'intersections (G, H, MC ...voir figure) peuvent donc être définis par leurs longitudes écliptiques (= distance angulaire entre ces points G, H, MC (voir figure) et le point gamma (voir figure)).. . Ces valeurs dépendent bien évidemment de l'inclinaison de l'écliptique sur l'horizon et donc de la latitude du lieu.
3) La question posée concerne la détermination de la longitude écliptique de ces points avec un astrolabe universel. Or, par définition, ces astrolabes ne sont pas liés à la latitude (contrairement au astrolabes "classiques" = planisphériques). Il faut donc évidemment "introduire" cette latitude locale dans la procédure pour utiliser l'instrument et s'en servir pour calculer les longitudes écliptiques des intersections entre l'écliptique et les limites des maisons locales.
C'est cette méthode que décrit rapidement Bion et que Seb. essaye d’éclaircir.
J'espère que ces quelques remarques éclairent un peu le débat.. amicalement !
Re: latitude équivalente
Posté : dim. 27 janv. 2019 11:28
par sebB
bonjour,
Merci à Yvon et à Eric pour leurs réponses.


j'ai trois questions.
question 1 : sait-on qui a mis au point le tracé d'un cadran solaire par la méthode du CHE?
question 2 : depuis quand cette méthode existe?
question 3 : si on lit le texte de Nicolas Bion, on remarque qu'il ne donne aucune méthode pour trouver la latitude équivalente. Est-ce que les astrolabes universelles étaient en mesure de résoudre ce type de problème ?
D'ailleurs existait-il des méthodes permettant de trouver la longitude équivalente et la latitude équivalente sans trigonométrie?
Merci
Re: latitude équivalente
Posté : dim. 27 janv. 2019 16:05
par Eric_M
En ce qui concerne les
question 1 : sait-on qui a mis au point le tracé d'un cadran solaire par la méthode du CHE?
question 2 : depuis quand cette méthode existe?
Je n'ai pas de réponse définitive, mais il est certain que Thabit ibn Qurra (826-901), un important auteur arabe, avait déja montré que n'importe quel cadran était l'équivalent d'un cadran horizontal situé ailleurs sur Terre... mais il n'est pas certain (à ma connaissance) que cette démonstration soit passée dans le mode latin, où elle a sans doute été redécouverte plus tard ...
Mais à mon avis, dès que l'on a compris que la Terre était une sphère, cette méthode s'impose d'elle même (??)
Re: latitude équivalente
Posté : dim. 27 janv. 2019 16:58
par Eric_M
En relisant ce que j'ai écrit il y a deux jours (message #108), il me semble qu'il manque encore une explication pour être parfaitement clair (au moins complet). La voila:
4) Les planètes (au sens médiéval) se baladent grosso-modo sur l'écliptique; or les éphémérides donnent pour chaque jour la longitude écliptique de chaque planète.
En connaissant les longitudes écliptiques de chaque intersection maisons/écliptique pour un lieu déterminé, on peut très rapidement et par lecture directe sur l'éphéméride, déterminer la maison qui accueille chacune des planètes.
D'où, la nécessité de connaitre les longitudes écliptiques des intersections des limites de maison avec l'écliptique (CQFD).
NB, il est clair que tout cela a des motivations purement astrologiques, il s'agit ici de déterminer l'horoscope de quelqu'un selon le jour mais aussi le lieu de sa naissance ..
Re: latitude équivalente
Posté : dim. 27 janv. 2019 18:53
par Yvon_M
En complément de la réponse d’Éric, pour ce qui concerne la 3ième question de Seb :
Comme l’astrolabe universel permet de résoudre le triangle de position (triangle formé par le pôle nord, le zénith et un astre quelconque ; les angles associés étant : angle horaire, latitude, déclinaison astronomique, hauteur et azimut) alors il peut déterminer la latitude équivalente (et de façon générale résoudre tout triangle sphérique) en faisant les associations suivantes :
Triangle de position -> Triangle du CHE
Latitude -> latitude
Angle horaire -> différence de longitude CHE / cadran
Azimut -> déclinaison gnomonique
Hauteur -> complément à 90° de l’inclinaison
Déclinaison astronomique -> latitude équivalente
La figure géométrique permettant de résoudre les triangles sphériques est l’analemme mais je ne sais pas si cette méthode a vraiment été utilisée. Elle est toutefois mentionnée avec d’autres précisions intéressantes sur le CHE par Montucla en appendice de ses
Récréations mathématiques, tome 3 ,
p. 293
Bon courage pour votre étude.
Re: latitude équivalente
Posté : dim. 27 janv. 2019 19:54
par sebB
j'ai tenté de résoudre le problème de Nicolas Bion en utilisant sa méthode du CHE par le calcul. Je verrai ensuite avec l'astrolabe universel.
alors voilà ma méthode.
coordonnées locales : phi = 49° et longitute = -3,312° pour le 12/01/2018
on fait les calculs pour 8 heures solaires soit H = -60°
on utilise la formule suivante pour calculer la longitude écliptique de l'ascendant (livre D. Savoie "cosmographie P 122).
tan (long_ascendant) = -cos(TS)/(tan(phi)*sin(epsi)+cos(epsi)*sin(TS)).
TS étant l'heure sidérale TS = H+ascension_droite
epsi est l'obliquité de l'écliptique soit 23,44°
après calcul on trouve
ascension droite = 294°
TS = 234°
long_ascendant = 295,85°
jusqu'ici pas de problème.



ensuite je vais utiliser la méthode du CHE pour déterminer la longitude écliptique du point d'intersection entre la maison céleste inclinée de 30° par rapport à l'horizon et l'écliptique.
j'ai calculé la latitude et la longitude équivalente de ce plan en utilisant le formulaire donnée par Eric.
pour ce plan Z=30° et D=90°.
en effet, il existe un plan horizontal équivalent à ce plan. Il suffit alors de calculer la longitude écliptique de l'ascendant par rapport à ce plan.
j'ai trouvé phi_equi = 40,81° et long_equi = 38,03°
dans la formule, j'ai remplacé phi par phi_equ mais est-ce que la longitude équivalente intervient dans le calcul???


Merci
Re: latitude équivalente
Posté : dim. 27 janv. 2019 20:15
par sebB
Merci Yvon et Eric pour vos interventions constructives.


j'ai feuilleté les pages relatives au CHE de Ozaman.
je vais sûrement y trouver des informations intéressantes pour résoudre mon problème.
Merci



