Je vous propose une petite énigme
Le propriétaire d'un château possède un joli parc dans lequel on trouve des allées et des parterres de fleurs légèrement en pente.
Ce jardin se visite et pour attiser la curiosité des visiteurs il souhaite installer sur l'une des pentes un cadran solaire gravé sur une dalle en pierre de taille. Pour cela, il fait appel à un ami maçon pour le tracer et la réalisation du cadran.
En se rendant à l'endroit où il doit réaliser le cadran, le maçon se rend compte rapidement que c'est un plan incliné déclinant.
IL relève la latitude du château phi = 50° et doit mesurer l'inclinaison Z et la déclinaison D du plan.
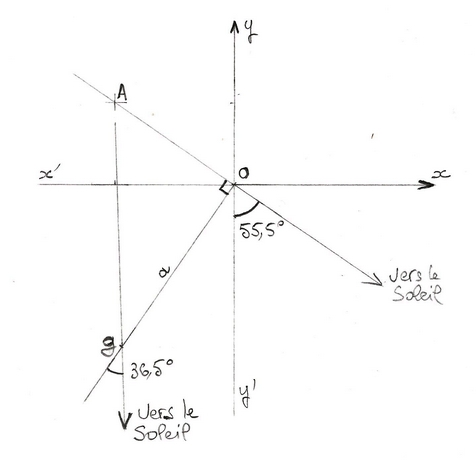
Pour effectuer ces mesures , au matin du 20 Avril il place une planchette munie d'un style droit de hauteur a = 50 mm et d'un repère orthogonal. Sur la planchette O est le point d'implantation du style droit, l'axe des abscisses Ox est orienté vers la droite et l'axe des ordonnées Oy est orienté vers le haut.
Il positionne la planchette de façon à ce que l'axe Oy soit orienté selon la ligne de plus grande pente du plan et vers le haut.
En ce jour le temps est incertain
Le point A a pour coordonnées x = -30,5 mm et y = 20,5 mm.
il mesure également l'inclinaison du plan Z à l'aide d'un inclinomètre. Z = 35°
Cependant, il ne sait pas déterminer la déclinaison du plan incliné déclinant.
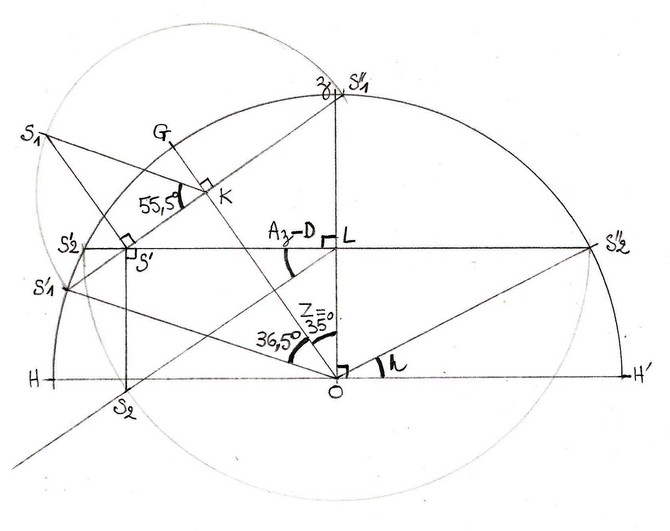
Sauriez vous aider le maçon à retrouver géométriquement la déclinaison D du plan ?
on respectera les contraintes suivantes :
on utilisera pas le formulaire permettant de déterminer Z et D à partir des coordonnées x et y du point A, ni la formule reliant Z et D!
on utilisera le matériel de géométrie.
Le seul calcul trigonométrique sera le calcul de l'azimut du soleil.