Le quadrant ancien : figure extraite de Protomathesis d’O. Fine, numérisation e-rara.
Dans cette nouvelle discussion je vous proposerai de retrouver le tracé de cet instrument avec un outil mathématique que vous connaissez bien mais qui est aujourd’hui un peu délaissé. Il était toutefois parfaitement maîtrisé par les inventeurs de ce quadrant que l’on s’accorde aujourd’hui à situer dans le monde Arabe de la fin du premier millénaire. Cet outil est, vous l’avez compris, la géométrie.
Les heures temporaires, ou antiques ou encore inégales, étaient en usage jusqu’à la fin du Moyen-Âge. Leur durée variait en fonction des saisons car il y avait exactement 12 heures dans une journée. Elles était décomptées depuis le lever du Soleil et il était 12 h à son coucher.
Si on imagine que le Soleil se déplace sur une sphère, sa course diurne décrit un arc de cercle. Aux équinoxes, cet arc est un demi-cercle. Il est plus grand au printemps et en été, plus petit en automne et en hiver. Les variations de grandeur de l’arc au cours des saisons sont d’autant plus importantes que la latitude est élevée. À l’équateur, la variation est nulle et le Soleil décrit toute l’année des demi-cercles.
Devant la multiplicité de ces cas de figure et dans l’optique d’aboutir à un instrument universel, les inventeurs du quadrant ancien ont pu imaginer de ramener les différentes courses du Soleil à une configuration unique en acceptant une certaine erreur si, bien sûr, elle est raisonnable. La configuration très simple et qui est le cas moyen pour toutes les latitudes est bien sûr le demi-cercle. Celui-ci doit toutefois être ajusté à la course réelle du Soleil. En prenant un rayon tel que le demi-cercle débute sur l’horizon et passe par la position du Soleil à 6 h, on a au moins, pour cette heure et les heures extrêmes de la journée, une correspondance exacte. Voyons ce qu’il en est pour les autres heures en se plaçant dans l’optique de ne mesurer que la hauteur du Soleil.
Sur la figure suivante la course du Soleil est tracée en rouge pour le solstice d’été à une latitude de 40° en regardant dans la direction du pôle sud. Le demi-cercle associé est tracé en bleu et il est divisé en 12 parties égales de 15°. Le renvoi de ces divisions vers le cercle rouge permet d’apprécier l’erreur qui sera commise et qui ne dépasse pas, dans ce cas, 10 min d’heure temporaire.
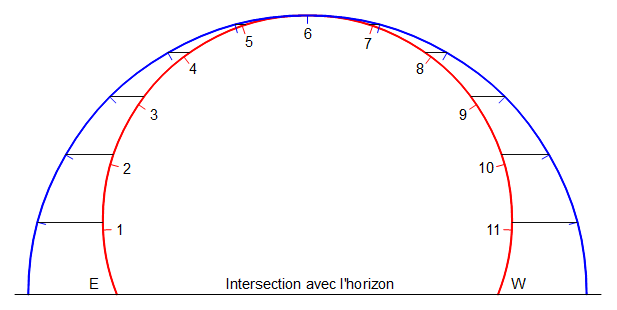
Figure 1
Pour le solstice d’hiver on obtient cette seconde figure avec une erreur encore plus faible :
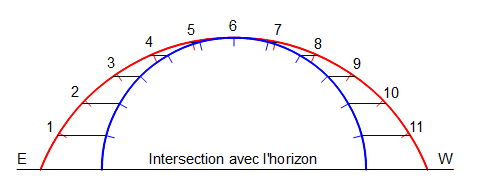
Figure 2
Ce n’est pas si mal ! Du moins les inventeurs du quadrant ancien se sont contenté de cette approximation car, nous le verrons ensuite, elle apporte des propriétés intéressantes qui conduisent à la réalisation d’un instrument extrêmement simple et facile à tracer.
Résumons cette approximation en projetant l’ensemble de la sphère céleste locale perpendiculairement sur le plan du méridien en suivant la technique graphique connue depuis l’Antiquité : l’analemme. Cette projection sera différente pour chaque latitude mais le raisonnement que nous allons établir sera valable dans tous les cas.
La course du Soleil pour une date donnée se projette suivant un segment de droite que nous appellerons segment diurne. Sur la figure 3 sont représentés les segments diurnes correspondant aux jours de l’entrée du Soleil dans les différents signes du zodiaque.
Les courbes rouges correspondent à la position réelle du Soleil pour toutes ses déclinaisons et aux différentes heures temporaires. Les courbes bleues correspondent à l’approximation que nous avons effectuée. Ces dernières ont la propriété évidente et particulièrement intéressante de diviser tous les segments diurnes suivant les mêmes proportions.
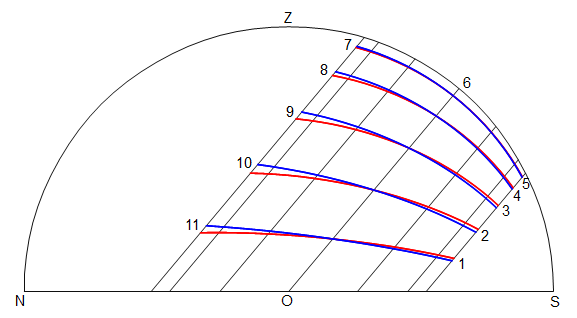
Figure 3
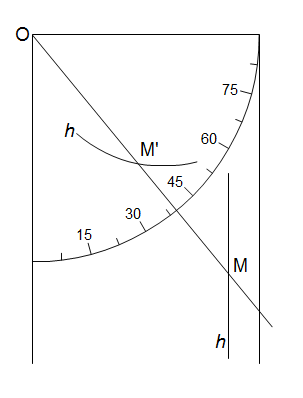
Intéressons-nous à un cas particulier tout en gardant à l’esprit que le raisonnement restera valable pour toutes les déclinaisons. Prenons, par exemple, le segment diurne de l’entrée dans le Taureau et cherchons comment obtenir l’angle de la hauteur du Soleil pour les différentes heures approchées et représentées par les courbes bleues. On comprendra facilement qu’il faut reporter leurs intersections avec le segment diurne du Taureau, parallèlement à l’horizon, jusqu’au cercle du méridien et tirer ensuite, du centre O, un rayon OP qui viendra rejoindre sur le méridien l’intersection correspondant à l’heure considérée, 2 ou 10 h dans le cas de la figure 4. La hauteur du Soleil cherchée sera alors l’angle h entre l’horizon et le rayon OP.
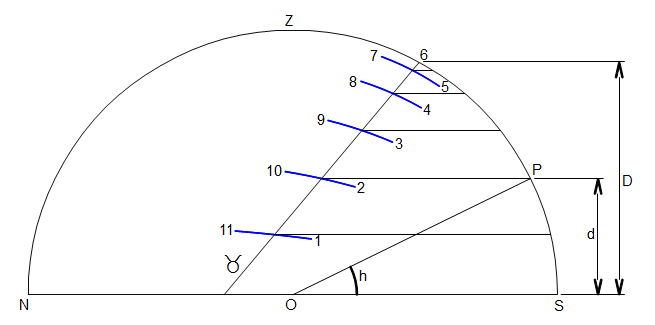
Figure 4
Il est à noter que, quelles que soient la latitude et la déclinaison du Soleil, la répartition des reports horizontaux, c’est-à-dire par exemple le rapport d/D pour 2 ou 10 h, sera toujours identique. Seul l’écartement total D sera différent et correspondra à la hauteur maxi du Soleil pour le jour concerné.
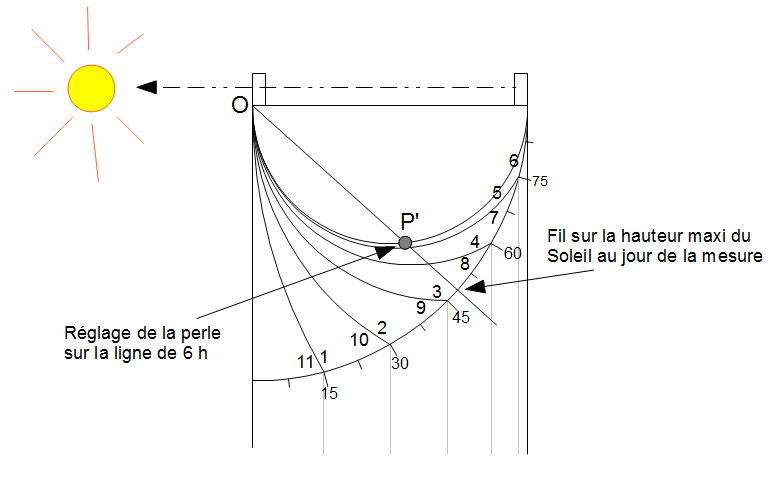
En imaginant de faire tourner la figure précédente d’un quart de tour dans le sens horaire, on est conduit naturellement à imaginer l’instrument suivant où un fil suspendu au point O fait parcourir à une perle P l’arc du méridien de l’analemme.
Pour régler la position de la perle, il suffit de se placer dans le cas de la hauteur maxi du Soleil, qu’il faut connaître par ailleurs, et placer la perle sur la ligne de 6 h. L’utilisation du cadran est ensuite identique à celle du Capucin.
Le quart de cercle gradué qui donne la hauteur du Soleil permet aussi de tracer les lignes horaires, il correspond en quelque sorte à la moitié des demi-cercles que nous avons utilisés dès le début pour l’approximation des heures temporaires.
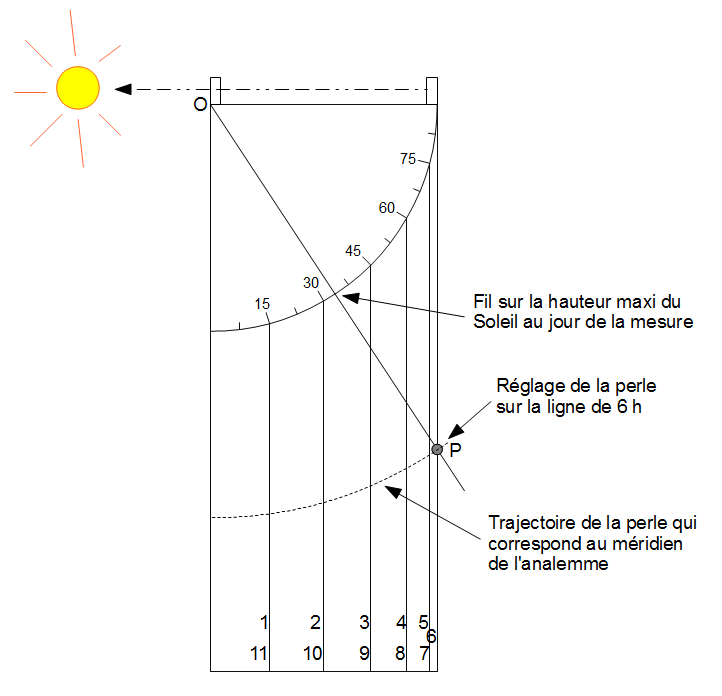
Figure 5
Très bien, me direz-vous, nous avons obtenu un instrument simple mais qui semble bien éloigné du quadrant ancien…
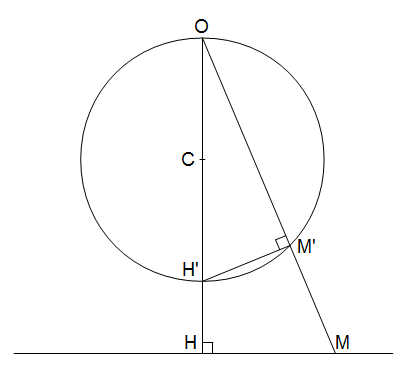
Rassurez-vous : nous n’en avons jamais été aussi près ! Il nous reste à donner un petit coup de baguette magique qui porte le nom moderne d’inversion géométrique.
J’aborderai ce point dans un prochain message pour vous laisser le temps de bien comprendre ce que je vous ai présenté et, au cas où, me poser des questions si certains points n’étaient pas suffisamment clairs.