cadran de hauteur "sabot à voile"

[sebB]

Bonjour à tous,

Lors de mes lectures du livre d'Yvon intitulé "de l'analemme aux cadrans de hauteurs", j'avais trouvé ce livre très intéressant et je m'étais posé des questions sur certains cadrans solaires, notamment le "sabot à voile".

Il est présenté à la page 53 et voici les illustrations:

sabot à voile.jpg (135.91 Kio) Vu 9608 fois

il est également écrit que :
Ce cadran est un subtil mélange des cadrans précédents avec la
particularité de simplifier le réglage de la perle en le ramenant, dans tous les cas, à la pointe du sabot. Toutes les lignes utiles restent cependant droites, ce qui fait que ce cadran appartient de plein droit à la famille des
cadrans rectilignes.

je pense que c'est un mélange entre le "capucin de saint rigaud" et le "cadran universel d'Apian".

J'ai trois questions :
question 1 : comment se trace ce cadran solaire ?
question 2 : comment justifier que le réglage de la perle se ramène à la pointe du sabot?
question 3 : comment justifier que les lignes horaires restent droites ?

Merci
Sébastien

[Yvon_M]

La façon la plus simple de comprendre ce cadran est de l’imaginer correspondant à la superposition de plusieurs capucins (comme celui représenté en vert sur la figure suivante) tracés pour différentes latitudes. Ainsi, Seb, en s’appuyant sur le principe du capucin on répond à tes 3 questions en même temps.



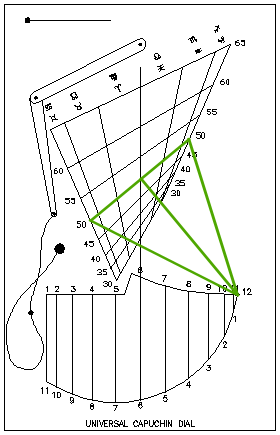
Mais on pourrait s’en poser une quatrième : pourquoi les courbes reliant les différents points de suspension du fil pour une même déclinaison sont des droites ?

Sur la figure suivante, P est la pointe du sabot et CA le prolongement de la ligne horaire de 6 h. Prenons CP pour unité et cherchons la courbe reliant les différents points de suspension pour la déclinaison d. Le point D fait partie de la courbe, c’est le point de suspension pour un cadran utilisé à l’équateur et on a CD = tan d.



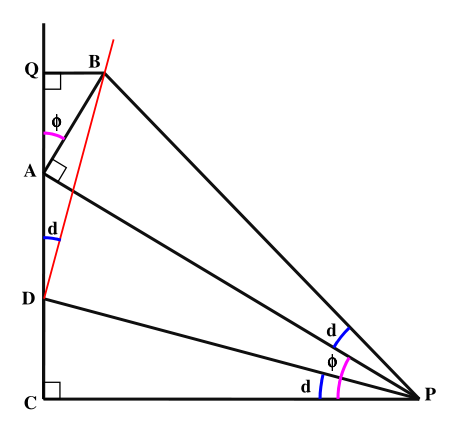
À la latitude ϕ, le point de suspension est en B avec AB = tan d/cos ϕ. Soit Q la projection orthogonale de B sur CA. Comme BA \(\perp\) AP et AC \(\perp\) CP, QAB = ϕ et par suite QA = tan d et QB = tan ϕ.tan d.

Par ailleurs : QD = QA + AC – CD = tan d + AC – tan d = AC = tan ϕ = QB/tan d,
ou encore : QB = QD.tan d

Ainsi, pour tout angle ϕ, le point B s’écarte de Q proportionnellement à la distance QD du facteur tan d, l’ensemble des points B est donc sur une droite qui fait un angle d avec CA.

Ce qui est intéressant de remarquer, c’est que si on fait glisser verticalement chacune de ces droites en l’associant au point de réglage de la perle et de façon à rassembler l’ensemble des points D en C, on retrouve le cadran de Regiomontanus.

[sebB]

Bonjour,

Merci Yvon pour ta réponse. C'est très clair et j'ai bien compris.

sebB