Bonjour,
En suivant les instructions de Denis Savoie dans son livre La Gnomonique (Les Belles Lettres), j'ai tracé un diagramme stéréographique.
Ce tracé, réalisé pour une latitude donnée, permet notamment de prévoir les périodes d'éclairement d'un cadran solaire plan (ou d'un mur), au fil de la journée et de l'année.
Comme son nom l'indique, ce diagramme est le résultat d'une projection stéréographique des cercles de la sphère céleste, avec l'équateur en guise de plan de projection, et le pôle Sud comme point de projection. Par conséquent, les arcs diurnes d'égale déclinaison apparaissent comme des cercles concentriques.
Dans l'image ci-jointe, la déclinaison du plan est nulle (mur ou cadran méridional). Le plan est matérialisé par l'arc de couleur marron. Le grand cercle extérieur est l'horizon de l'observateur. Ici, on lit qu'au solstice d'été, le plan est éclairé de 7h30 à 16h30 environ.
Grâce aux lignes horaires (radiales), o y lit également les heures de lever et de coucher du Soleil (intersections des arcs diurnes avec l'horizon).
J'ai réalisé ce tracé avec LaTeX (et plus précisément l'extension TikZ). Dans le code (ci-joint), vous pouvez facilement modifier les valeurs de latitude, de déclinaison du cadran, ainsi que la distance zénithale pour les cadrans inclinés. Cependant, les limites de calcul de LaTeX sont atteintes pour certaines valeurs "extrêmes" de déclinaison (proche de 90°) ou de distance zénithale.
Si vous avez des idées d'amélioration, n'hésitez pas à les partager.
Diagramme stéréographique
Diagramme stéréographique
- Fichiers joints
-
- DiagStereographique.tex.zip
- le code LaTeX du fichier
- (1.96 Kio) Téléchargé 1803 fois
-
- DiagStereographique_495_0b.png (164.33 Kio) Vu 43371 fois
- Yvon_M
- Administrateur du site
- Messages : 402
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Diagramme stéréographique
Merci David pour nous proposer ce diagramme qui permet de traiter un problème sur lequel j’ai eu l’occasion de passer beaucoup de temps, j’y reviendrai plus tard.
En parcourant votre programme, j’ai été surpris par les relations qui déterminent le cercle du cadran. En effet, il n’y a pas de raison pour qu’elles soient différentes de celles qui servent à déterminer le cercle de l’horizon. En consultant Gnomonique moderne (je n’ai pas La Gnomonique, mais je suppose que le passage concernant ce diagramme est commun aux deux livres), j’ai bien retrouvé les mêmes relations et, en approfondissant, j’ai constaté qu’elles comportaient de petites erreurs.
Pour moi le rayon d’un cercle est une distance qui, par définition, est positive. La latitude équivalente \(f\) pouvant être négative, on doit écrire :
\[r_c=|\frac{R}{\sin f}|\]
Quant à \(PK\), \(P\) étant le pôle nord et \(K\) le centre du cercle, c’est une distance algébrique mesurée sur l'axe orienté suivant l’heure \(S \) de la sous-stylaire, il convient donc de l’écrire \(\overline{PK}\) avec :
\[\overline{PK}=\frac{R}{\tan f}\]
En plus, il faut considérer la règle suivante : si la latitude \(f\) est positive, c’est la partie concave du cercle qui correspond à l’avant du cadran. Si \(f\) est négative, c’est la partie convexe.
Il est aussi intéressant de noter que cette règle s’applique de la même manière au cercle de l’horizon et qu’il est donc possible d’utiliser ce diagramme pour l’hémisphère sud, sans changer la définition de la projection. Afin de prendre en compte les valeurs de \(\phi\) négatives, il faut donc écrire les relations du cercle de l’horizon de la même manière :
\[r_h=|\frac{R}{\sin \phi}| \qquad \overline{PM}=\frac{R}{\tan \phi}\]
\(\overline{PM}\) étant pris sur l’axe orienté de la ligne de midi. Voici ce que j’ai pu obtenir en prenant \(\phi = -42°\), \(D = 150°\) et \(z = 90°\). On obtient alors \(S = 40,79°\) et \(f = 40,06°\), le diagramme est le suivant :
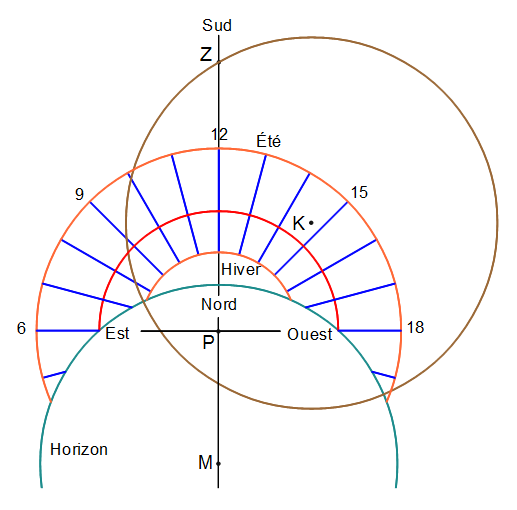
\(f\) étant positif, c’est donc à l’intérieur du cercle marron que l’on trouve les heures d’éclairement du cadran. On peut aussi remarquer qu’il faut inverser la dénomination hiver/été des solstices car dans l’hémisphère sud, le printemps et l’été ont lieu quand la déclinaison du Soleil est négative.
En parcourant votre programme, j’ai été surpris par les relations qui déterminent le cercle du cadran. En effet, il n’y a pas de raison pour qu’elles soient différentes de celles qui servent à déterminer le cercle de l’horizon. En consultant Gnomonique moderne (je n’ai pas La Gnomonique, mais je suppose que le passage concernant ce diagramme est commun aux deux livres), j’ai bien retrouvé les mêmes relations et, en approfondissant, j’ai constaté qu’elles comportaient de petites erreurs.
Pour moi le rayon d’un cercle est une distance qui, par définition, est positive. La latitude équivalente \(f\) pouvant être négative, on doit écrire :
\[r_c=|\frac{R}{\sin f}|\]
Quant à \(PK\), \(P\) étant le pôle nord et \(K\) le centre du cercle, c’est une distance algébrique mesurée sur l'axe orienté suivant l’heure \(S \) de la sous-stylaire, il convient donc de l’écrire \(\overline{PK}\) avec :
\[\overline{PK}=\frac{R}{\tan f}\]
En plus, il faut considérer la règle suivante : si la latitude \(f\) est positive, c’est la partie concave du cercle qui correspond à l’avant du cadran. Si \(f\) est négative, c’est la partie convexe.
Il est aussi intéressant de noter que cette règle s’applique de la même manière au cercle de l’horizon et qu’il est donc possible d’utiliser ce diagramme pour l’hémisphère sud, sans changer la définition de la projection. Afin de prendre en compte les valeurs de \(\phi\) négatives, il faut donc écrire les relations du cercle de l’horizon de la même manière :
\[r_h=|\frac{R}{\sin \phi}| \qquad \overline{PM}=\frac{R}{\tan \phi}\]
\(\overline{PM}\) étant pris sur l’axe orienté de la ligne de midi. Voici ce que j’ai pu obtenir en prenant \(\phi = -42°\), \(D = 150°\) et \(z = 90°\). On obtient alors \(S = 40,79°\) et \(f = 40,06°\), le diagramme est le suivant :

\(f\) étant positif, c’est donc à l’intérieur du cercle marron que l’on trouve les heures d’éclairement du cadran. On peut aussi remarquer qu’il faut inverser la dénomination hiver/été des solstices car dans l’hémisphère sud, le printemps et l’été ont lieu quand la déclinaison du Soleil est négative.
Yvon Massé - Site perso. : La gnomonique
Re: Diagramme stéréographique
Merci, Yvon, d'avoir pris le temps de regarder de près le calcul, et pour ces précisions. Notamment concernant l'utilisation pour l'hémisphère sud.
David
David
- Yvon_M
- Administrateur du site
- Messages : 402
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Diagramme stéréographique
Comme proposé, je voulais apporter un petit complément au problème des heures extrêmes vues par un cadran plan. D. Savoie, qui a consacré à ce sujet un chapitre de 15 pages dans la Gnomonique moderne, observe que « le cas des cadrans inclinés déclinants est lourd à traiter en globalité », c’est pourquoi il a proposé le diagramme que David nous a fait partager.
Il y a maintenant plus de 20 ans, je m’étais penché sur le problème et j’avais préféré utiliser un autre type de diagramme, avec des lignes horaires parallèles et dont les courbes de l’horizon et du cadran sont des sinusoïdes. Cela avait fait l’objet d’un petit programme sur calculette et d’un article que vous pouvez consulter ici :
http://cadrans-solaires.scg.ulaval.ca/c ... v5no3.html
Les moyens ont beaucoup évolué depuis, Geogébra nous permet maintenant de représenter ce diagramme de façon plus interactive :
En jouant sur les curseurs (allez-y, le diagramme est vraiment interactif et ce sont de vrais curseurs que vous pouvez manœuvrer à la souris) on peut voir comment évolue la zone blanche qui donne les heures où le cadran est éclairé en fonction de la déclinaison du Soleil, ou plus exactement de sa tangente. On peut constater que la zone violette est directement liée aux paramètres du cadran horizontal équivalent (CHE) : sa latitude f et sa différence de longitude S.
À l’époque, j’avais voulu aussi trouver un algorithme pour calculer directement les heures extrêmes d’éclairement en fonction des paramètres du cadran. Cela m’avait bien occupé l’esprit et comme le résultat était assez complexe, j’avais préféré le laisser sous forme d’un simple programme. Vous le retrouverez ici :
http://gnomonique.fr/gnomon/eclair.htm
En le reprenant pour vous le présenter, ce que je ferai dans un prochain message, j’ai constaté qu’on pouvait encore le simplifier. En attendant, je l’ai intégré dans ce message et vous pouvez l’utiliser avec le bouton ‘Calculer’ du tableau après avoir renseigné les valeurs d’entrée : latitude du lieu, déclinaison et inclinaison du cadran.
Bonne utilisation !
Il y a maintenant plus de 20 ans, je m’étais penché sur le problème et j’avais préféré utiliser un autre type de diagramme, avec des lignes horaires parallèles et dont les courbes de l’horizon et du cadran sont des sinusoïdes. Cela avait fait l’objet d’un petit programme sur calculette et d’un article que vous pouvez consulter ici :
http://cadrans-solaires.scg.ulaval.ca/c ... v5no3.html
Les moyens ont beaucoup évolué depuis, Geogébra nous permet maintenant de représenter ce diagramme de façon plus interactive :
En jouant sur les curseurs (allez-y, le diagramme est vraiment interactif et ce sont de vrais curseurs que vous pouvez manœuvrer à la souris) on peut voir comment évolue la zone blanche qui donne les heures où le cadran est éclairé en fonction de la déclinaison du Soleil, ou plus exactement de sa tangente. On peut constater que la zone violette est directement liée aux paramètres du cadran horizontal équivalent (CHE) : sa latitude f et sa différence de longitude S.
À l’époque, j’avais voulu aussi trouver un algorithme pour calculer directement les heures extrêmes d’éclairement en fonction des paramètres du cadran. Cela m’avait bien occupé l’esprit et comme le résultat était assez complexe, j’avais préféré le laisser sous forme d’un simple programme. Vous le retrouverez ici :
http://gnomonique.fr/gnomon/eclair.htm
En le reprenant pour vous le présenter, ce que je ferai dans un prochain message, j’ai constaté qu’on pouvait encore le simplifier. En attendant, je l’ai intégré dans ce message et vous pouvez l’utiliser avec le bouton ‘Calculer’ du tableau après avoir renseigné les valeurs d’entrée : latitude du lieu, déclinaison et inclinaison du cadran.
Bonne utilisation !
Yvon Massé - Site perso. : La gnomonique
- Yvon_M
- Administrateur du site
- Messages : 402
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Diagramme stéréographique
Voici donc la description de l’algorithme que j’ai utilisé pour calculer les heures extrêmes vues par un cadran plan quelconque, ce qui permet de limiter le tracer de ses lignes horaires aux seules heures utiles. Avec le graphique du message précédent, nous avons déjà noté que ces heures découlent directement des zones bleues et violettes qui répondent respectivement :
On remarquera que les heures extrêmes dépendent :
Il faut maintenant, et c’est la principale difficulté, agencer et regrouper les différentes configurations pour éviter les calculs redondants et définir la procédure la plus simple possible. J’ai finalement retenu l’algorithme suivant qui m’a semblé relativement épuré mais il en existe d’autres. Le principe est de se situer dans une des trois conditions principales suivantes et considérer ensuite les sous-cas de figure :
Si vous avez eu le courage de me lire jusqu’ici, j’espère que vous n’avez pas aussi mal à la tête que ce que j’ai enduré quand j’ai essayé de structurer cet algorithme 
Correction : à vouloir trop simplifier, j’ai introduit dans le 3ième cas des calculs anticipés qui ne sont pas toujours possibles, c’est maintenant rectifié.
Notes :
1 ^ On peut aussi traiter globalement le problème de l’éclairement uniquement du point de vue de l’hémisphère nord, par symétrie. Pour l’hémisphère sud il faut, dans ce cas, modifier les données d’entrée :
3 ^ Pour la France, c’est le cas des cadrans verticaux orientés vers l’occident.
4 ^ Pour la France, c’est le cas des cadrans verticaux orientés vers l’orient.
5 ^ Il n’y a que dans cette configuration qu’il est nécessaire d’évaluer les angles horaires \(Ah_{I1}\) et \(Ah_{I2}\). Pour éviter le cas où \(\phi = 0\), il suffit d’utiliser comme condition pour la différence de signe des latitudes : \(\phi\cdot f < 0\)
6 ^ Pour la France, c’est le cas de la face sud des cadrans équatoriaux et des cadrans verticaux orientés vers le sud.
7 ^ Le cas où \(|\phi|=|f|\), quel que soit \(S\), correspond au seul cas théorique où le cadran ne voit pas le Soleil : il est dirigé vers le sol (\(z=180°\)).
8 ^ Pour la France, c’est le cas des cadrans verticaux orientés vers le nord.
9 ^ C’est le cas des cadrans horizontaux quand \(|\phi|=|f|\). Pour la France, quand \(\phi\) et \(f\) sont différents, c’est le cas des cadrans faiblement inclinés vers le nord comme la face nord des cadrans équinoxiaux.
10 ^ Pour la France, c’est le cas des cadrans faiblement inclinés vers le sud.
- À l’horizon où est installé le cadran
- Au plan du cadran lui-même
- Pour l’horizon : \(\tan\delta=-\frac{\cos Ah}{\tan\phi}\)
- Pour le cadran : \(\tan\delta=-\frac{\cos (Ah-S)}{\tan f}\)
On remarquera que les heures extrêmes dépendent :
- du fait que les latitudes considérées, \(\phi\) ou \(f\), concernent les zones polaires, zones où le Soleil ne se couche pas à certaines saisons (d’accord, il n’y a pas beaucoup de cadran solaire au dessus du 67ième parallèle mais l’algorithme est censé prendre en compte tous les cas de figure). Il est possible de résumer cette situation par les conditions \(\cos\phi\leq\sin\epsilon\) et \(\cos f\leq\sin\epsilon\), \(\epsilon\) étant l'obliquité de l'écliptique.
- des heures de lever et de coucher du Soleil (bien sûr, quand on n’est pas dans la configuration précédente), sur l’horizon ou sur le plan du cadran, pour une déclinaison extrême du Soleil : \(\epsilon\) ou \(-\epsilon\) suivant le signe de \(\phi\) et \(f\). Les angles horaires correspondants s’obtiennent avec les relations suivantes :
- Pour le lever sur l’horizon : \(Ah_{lh} = -\arccos(-\tan |\phi|\cdot\tan\epsilon)\)
- Pour le coucher sur l’horizon : \(Ah_{ch} = \arccos(-\tan |\phi|\cdot\tan\epsilon)\)
- Pour le lever sur le cadran : \(Ah_{lc} = S - \arccos(-\tan |f|\cdot\tan\epsilon)\)
- Pour le coucher sur le cadran : \(Ah_{cc} = S + \arccos(-\tan |f|\cdot\tan\epsilon)\)
- de la position des points d’intersection des deux sinusoïdes dans le graphique. Ces points correspondent à l’endroit où la droite d’intersection de l’horizon et du plan du cadran perce la sphère céleste. Dans le repère local, l’azimut \(Az\) et la hauteur \(h\) de ces points sont simplement \(Az = D\pm 90°\) et \(h = 0\).
Appelons \(I1\) le point situé du côté où le Soleil se lève sur le cadran et \(I2\) le point du côté où il se couche. Dans l’hémisphère nord, \(Az = D - 90°\) pour \(I1\) et \(Az = D + 90°\) pour \(I2\). Par contre, dans l’hémisphère sud, le cadran vertical qui est tourné vers le Soleil de midi est un cadran plein nord, c’est-à-dire qu’il a une déclinaison de \(180°\). Quant à \(I2\), qui est à l’ouest comme dans l’hémisphère nord, son azimut est de \(90°\), il faut donc écrire \(Az =D - 90°\) pour \(I2\) et par suite \(Az = D + 90°\) pour \(I1\). Retenons simplement qu’il faut inverser les relations de \(I1\) et \(I2\) quand on passe dans l’hémisphère sud (1).
En revenant dans l’hémisphère nord et en utilisant les formules de passage dans le repère horaire, on obtient l’angle horaire \(Ah\) et la déclinaison \(\delta\) de ces points par les relations :- Pour \(I1\) : \(Ah = \arctan2(-\cos D, \sin\phi\cdot\sin D)\) et \(\delta_1 = -\arcsin(\cos\phi\cdot\sin D)\)
- Pour \(I2\) : \(Ah = \arctan2(\cos D, -\sin\phi\cdot\sin D)\) et \(\delta_2 = \arcsin(\cos\phi\cdot\sin D)\)
\(Ah_{I1} = \arctan2(-\cos D/\sin\phi, \sin D)\) et \(Ah_{I2} = \arctan2(\cos D/\sin\phi, -\sin D)\) quel que soit le signe de \(\phi\).
En toute rigueur, le seul inconvénient est que ces angles horaires ne sont pas définis pour \(\phi = 0\) mais nous verrons comment contourner ce problème. - enfin, de l’ampleur de la différence de longitude. Pour \(|S| > 90°\) (2) on peut effectivement rencontrer des situations où le cadran est éclairé à deux périodes dans la journée, c’est le cas classique du cadran vertical plein nord dans l’hémisphère nord.
- \(Ah_{min}\) qui correspond à l’heure extrême la plus précoce
- \(Ah_{max}\) pour l’heure extrême la plus tardive
- Éventuellement \(Ah_1\) et \(Ah_2\) respectivement pour l’heure la plus tardive de la première période d’éclairement du cadran et l’heure la plus précoce de la seconde période
Il faut maintenant, et c’est la principale difficulté, agencer et regrouper les différentes configurations pour éviter les calculs redondants et définir la procédure la plus simple possible. J’ai finalement retenu l’algorithme suivant qui m’a semblé relativement épuré mais il en existe d’autres. Le principe est de se situer dans une des trois conditions principales suivantes et considérer ensuite les sous-cas de figure :
- Les points \(I1\) et \(I2\) sont en dehors du graphique ou encore \(|\delta_2| = |\arcsin(\cos\phi\cdot\sin D)|\geq\epsilon\). Cette situation ne peut se présenter que si les latitudes \(\phi\) et \(f\) sont toutes les deux hors des zones polaires. C’est alternativement l’horizon et le cadran qui détermine les heures extrêmes suivant le signe de \(S\) :
- Les points \(I1\) et \(I2\) sont à l’intérieur du graphique et les latitudes \(\phi\) et \(f\) sont de signe contraire (5). Dans cette configuration les heures extrêmes correspondent en général à l’angle horaire des points \(I1\) et \(I2\) :
\(Ah_{min} = Ah_{I1}\) et \(Ah_{max} = Ah_{I2}\) (6)
sauf dans le cas particulier où les latitudes \(\phi\) et \(f\) sont toutes les deux hors des zones polaires et \(|S| > 90°\). Il y a alors deux périodes d’éclairement qui sont de nature différente suivant les valeurs relatives de \(\phi\) et \(f\) (7) :- Si \(|\phi| < |f|\) : les heures déterminées pour le cas général sont correctes et il faut calculer en plus les heures intermédiaires \(Ah_1 = Ah_{cc}\) et \(Ah_2 = Ah_{lc}\)
- Si \(|\phi| > |f|\) : les heures déterminées pour le cas général sont en fait les heures intermédiaires \(Ah_1 = Ah_{I2}\) et \(Ah_2 = Ah_{I1}\). Quant aux heures extrêmes, elles correspondent aux angles horaires \(Ah_{min} = Ah_{lh}\) et \(Ah_{max} = Ah_{ch}\)
- Les points \(I1\) et \(I2\) sont à l’intérieur du graphique et les latitudes \(\phi\) et \(f\) sont de même signe. Il faut vérifier dans l'ordre les configurations suivantes :
- Si les latitudes \(\phi\) et \(f\) sont toutes les deux situées dans les zones polaires, le cadran est éclairé toute la journée.
- Si les latitudes \(\phi\) et \(f\) sont toutes les deux hors des zones polaires et \(|S| > 90°\), il y a deux périodes d’éclairement. Les heures extrêmes correspondent dans l’ordre à \(Ah_{min} = Ah_{lh}\), \(Ah_1 = Ah_{cc}\), \(Ah_2 = Ah_{lc}\) et \(Ah_{max} = Ah_{ch}\) (8).
- Si \(|\phi|\leq|f|\), c’est l’horizon qui limite l’éclairement et les heures extrêmes correspondent à \(Ah_{min} = Ah_{lh}\) et \(Ah_{max} = Ah_{ch}\) (9)
- Sinon, c’est le cadran qui limite son éclairement et les heures extrêmes correspondent à \(Ah_{min} = Ah_{lc}\) et \(Ah_{max} = Ah_{cc}\) (10)
Code : Tout sélectionner
# coding: utf-8
from math import *
def conv_h(ah):
# Retourne l'heure correspondant à l'angle horaire d'entrée
m = round((ah*12/pi + 12)*60) # Nombre de minutes
h = floor(m/60) # Nombre d'heures entières
m -= 60*h # Nombre de minutes restantes
return '%02d h %02d'%(h, m)
def coulev(la, lo, cl):
ah = acos(-tan(abs(la))*tan(eps))
if cl:
ah = lo - ah
if ah <= -pi: ah += 2*pi
else:
ah = lo + ah
if ah > pi: ah -= 2*pi
return ah
# Constantes et initialisations
dr = pi/180 # Pour la conversion degré / radian
eps = 23.437*dr # Obliquité de l'écliptique
Ah_1 = 5 # Pas d'heures intermédiaires
# Saisie des paramètres
phie = input('Latitude en deg. ? ')
phi = float(phie)*dr
De = input('Declinaison en deg. ? ')
D = float(De)*dr
ze = input('Inclinaison en deg. ? ')
z = float(ze)*dr
# Latitude et différence de longitude du CHE
f = asin(sin(phi)*cos(z) - cos(phi)*cos(D)*sin(z))
S = atan2(sin(D)*sin(z), cos(phi)*cos(z) + sin(phi)*cos(D)*sin(z))
if abs(asin(cos(phi)*sin(D))) >= eps:
if S > 0:
Ah_min = coulev(f, S, True)
Ah_max = coulev(phi, 0, False)
else:
Ah_min = coulev(phi, 0, True)
Ah_max = coulev(f, S, False)
else:
if phi*f < 0:
Ah_min = atan2(-cos(D)/sin(phi), sin(D))
Ah_max = atan2(cos(D)/sin(phi), -sin(D))
if cos(phi) > sin(eps) and cos(f) > sin(eps) and abs(S) > pi/2:
if abs(phi) < abs(f):
Ah_1 = coulev(f, S, False)
Ah_2 = coulev(f, S, True)
else:
Ah_1 = Ah_max
Ah_2 = Ah_min
Ah_min = coulev(phi, 0, True)
Ah_max = coulev(phi, 0, False)
else:
if cos(phi) <= sin(eps) and cos(f) <= sin(eps):
Ah_min = -pi
Ah_max = pi
else:
if cos(phi) > sin(eps) and cos(f) > sin(eps) and abs(S) > pi/2:
Ah_min = coulev(phi, 0, True)
Ah_1 = coulev(f, S, False)
Ah_2 = coulev(f, S, True)
Ah_max = coulev(phi, 0, False)
else:
if abs(phi) <= abs(f):
Ah_min = coulev(phi, 0, True)
Ah_max = coulev(phi, 0, False)
else:
Ah_min = coulev(f, S, True)
Ah_max = coulev(f, S, False)
# Affichage des résultats
print('H. min = '+conv_h(Ah_min))
if Ah_1 != 5:
print('Int. 1 = '+conv_h(Ah_1))
print('Int. 2 = '+conv_h(Ah_2))
print('H. max = '+conv_h(Ah_max))Correction : à vouloir trop simplifier, j’ai introduit dans le 3ième cas des calculs anticipés qui ne sont pas toujours possibles, c’est maintenant rectifié.
Notes :
1 ^ On peut aussi traiter globalement le problème de l’éclairement uniquement du point de vue de l’hémisphère nord, par symétrie. Pour l’hémisphère sud il faut, dans ce cas, modifier les données d’entrée :
- Utiliser la latitude équivalente \(\phi_e = |\phi|\)
- Utiliser la déclinaison gnomonique équivalente : \(D_e = 180° – D\)
- Utiliser l’inclinaison sans modification
3 ^ Pour la France, c’est le cas des cadrans verticaux orientés vers l’occident.
4 ^ Pour la France, c’est le cas des cadrans verticaux orientés vers l’orient.
5 ^ Il n’y a que dans cette configuration qu’il est nécessaire d’évaluer les angles horaires \(Ah_{I1}\) et \(Ah_{I2}\). Pour éviter le cas où \(\phi = 0\), il suffit d’utiliser comme condition pour la différence de signe des latitudes : \(\phi\cdot f < 0\)
6 ^ Pour la France, c’est le cas de la face sud des cadrans équatoriaux et des cadrans verticaux orientés vers le sud.
7 ^ Le cas où \(|\phi|=|f|\), quel que soit \(S\), correspond au seul cas théorique où le cadran ne voit pas le Soleil : il est dirigé vers le sol (\(z=180°\)).
8 ^ Pour la France, c’est le cas des cadrans verticaux orientés vers le nord.
9 ^ C’est le cas des cadrans horizontaux quand \(|\phi|=|f|\). Pour la France, quand \(\phi\) et \(f\) sont différents, c’est le cas des cadrans faiblement inclinés vers le nord comme la face nord des cadrans équinoxiaux.
10 ^ Pour la France, c’est le cas des cadrans faiblement inclinés vers le sud.
Yvon Massé - Site perso. : La gnomonique