D'après une idée proposée par Jorge Ramalho
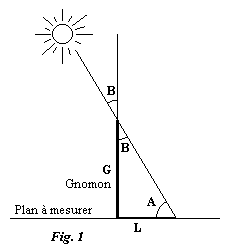
La connaissance de la longueur de l'ombre du gnomon nous permet de calculer la hauteur A du soleil au dessus du plan à mesurer (Fig. 1). Nous pouvons écrire:
tg A = G/Lou encore:
sin A = cos B = G/Rac (G² + L²) (1)

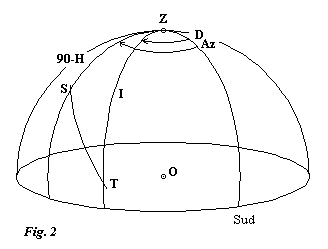
Représentons, figure 2, la sphère céleste de centre O. Soient Z le zénith, S la position du soleil et T le prolongement du gnomon. Nous avons un triangle sphérique dont nous connaissons deux cotés: ZS correspond au complément de la hauteur H du soleil au dessus de l'horizon et ZT à l'inclinaison I du plan. Enfin, remarquons que ST correspond à l'angle B de la figure 1.
Les relations des triangles sphériques nous donnent:
cos ST = cos B = cos (90° - H).cos I + sin (90° - H).sin I.cos (Az - D)D'après (1) on obtient:
G/Rac (G² + L²) - sin H.cos I
cos (Az - D) = -------------------------------
cos H.sin I
G/Rac (G² + L²) - sin H.cos I
D = Az ± Arccos (-------------------------------)
cos H.sin I
Le signe de l'Arccos dépend de la position de l'ombre par rapport à la ligne de plus grande pente qui passe par le pied du gnomon. Si l'ombre est à gauche en regardant la planchette, il faut ajouter l'Arccos et si elle est à droite, bien sûr, il faut le soustraire.
G/Rac (G² + L²)
D = Az ± Arccos (-----------------)
cos H
Le programme d'application proposé ci-dessous est écrit pour Qbasic de Microsoft mais il est facilement adaptable à tout autre langage.
Remarque: Ce programme est valable en tout point du globe sans aucune modification.
REM Constantes
k = .0172024
jm = 674.03
jl = 752.2
e = .0167
ob = .4091
pi = 3.141593: dr = pi / 180: hr = pi / 12
REM Fuseau horaire et coordonnées géographiques
INPUT "Fuseau horaire"; fh
INPUT "Longitude (en degré, positive à l'ouest)"; lo: lo = lo * dr
INPUT "Latitude (en degré)"; la: dp = (90 - la) * dr
REM Date
INPUT "Jour, Mois, Année"; jo, mo, an
IF mo < 3 THEN mo = mo + 12: an = an - 1
INPUT "Heure (légale), Minute"; hh, mn
REM Nombre de jours écoulés depuis
REM le 1 Mars O h TU de la dernière année bissextile + 2 ans
h = hh + mn / 60 - fh
j = 365 * (an - 4 * INT(an / 4)) + INT(30.61 * (mo + 1)) + jo + h / 24 - 853
REM Longitude vraie du soleil
m = k * (j - jm): l = k * (j - jl)
s = l + 2 * e * SIN(m) + 1.25 * e * e * SIN(2 * m)
REM Coordonnées locales du soleil
x = COS(s): y = COS(ob) * SIN(s): z = SIN(ob) * SIN(s)
r = l + h * hr - lo - pi: GOSUB 1300: r = dp: GOSUB 1200
REM Correction de la réfraction
ht = asin(z): rf = 0
IF ht < 1.56 THEN rf = .000291 / TAN(ht + .00223 / (ht + .077))
REM Hauteur et azimut du soleil
ht = ht + rf
az = angl(x, -y)
REM Affichage de la position du soleil en degrés
PRINT "Azimut="; az / dr
PRINT "hauteur="; ht / dr
INPUT "Hauteur du gnomon"; g
INPUT "Longueur de l'ombre (dans la même unité)"; lg
INPUT "Inclinaison du plan (90° pour un mur vertical)"; i: i = i * dr
dl = acos((g / SQR(g * g + lg * lg) - SIN(ht) * COS(i)) / COS(ht) / SIN(i))
REM affichage des résultats en degrés
PRINT
PRINT "En regardant la planchette, par rapport à la ligne"
PRINT "de plus grande pente passant par le pied du gnomon"
PRINT "si l'ombre est à gauche: d="; (az + dl) / dr
PRINT "si l'ombre est à droite: d="; (az - dl) / dr
END
1200 REM Rotation de l'angle r autour de l'axe y
rx = COS(r) * x - SIN(r) * z: rz = SIN(r) * x + COS(r) * z
x = rx: z = rz: RETURN
1300 REM Rotation de l'angle r autour de l'axe z
rx = COS(r) * x + SIN(r) * y: ry = -SIN(r) * x + COS(r) * y
x = rx: y = ry: RETURN
FUNCTION acos (x)
REM Fonction Arc Cosinus
SHARED pi
IF x = 0 THEN
a = pi / 2
ELSE
a = ATN(SQR(1 - x * x) / x)
IF x < 0 THEN a = a + pi
END IF
acos = a
END FUNCTION
FUNCTION angl (x, y)
REM Angle d'un vecteur par rapport à l'axe des x
SHARED pi
IF x = 0 THEN
a = SGN(y) * pi / 2
ELSE
a = ATN(y / x)
IF x < 0 AND y >= 0 THEN a = a + pi
IF x < 0 AND y < 0 THEN a = a - pi
END IF
angl = a
END FUNCTION
FUNCTION asin (y)
REM Fonction Arc Sinus
SHARED pi
IF ABS(y) = 1 THEN asin = y * pi / 2 ELSE asin = ATN(y / SQR(1 - y * y))
END FUNCTION
Retour à la page d'accueil -o- Reveno al la akcepta retpagho
Date de création: 21 Février 2000
Date de la dernière mise à jour: 28 Octobre 2000 (Merci Guido)