Dans cette troisième et dernière partie j’aborderai la façon dont j’ai intégré la méthode des 2 points d’ombre dans le programme Calcad que l’on peut
télécharger ici. J’ai baptisé ce type de programme « échangiciel » car il est entièrement gratuit d’utilisation mais, si Calcad est utilisé pour réaliser un cadran, je demande en échange une simple photo du cadran réalisé.
C’est la puissance de la méthode des 2 points d’ombre, qui permet de tracer sans distinction tous les types de cadran plan (horizontal, verticaux, inclinés déclinants), et le fait qu’elle ne demande pratiquement aucune donnée d’entrée propre à la gnomonique (position géographique, inclinaison et déclinaison du plan) qui m’a poussé à la moderniser et à l’intégrer dans ce programme à l’attention des débutants, le but étant de leur éviter l’acquisition de connaissances spécifiques et complexes. Les options qui ont été retenues pour le développement de Calcad découlent ainsi de la seule volonté de ne pas faire appel à des notions propres à la gnomonique quand elles ne sont pas nécessaires.
Parmi les mesures modernes qui peuvent être facilement ajoutées au mode opératoire de la méthode des 2 points d’ombre, il y a les heures \(H_1\) et \(H_2\) à l’instant du relevé des 2 points. L’heure, qui était difficilement disponible à l’époque de La Hire, est de nos jours facilement accessible avec la plus grande précision. Il est aussi demandé de saisir la date et, pour être dans le cas le plus général, les dates de chaque relevé, \(j_1\) et \(j_2\), pourront être différentes.
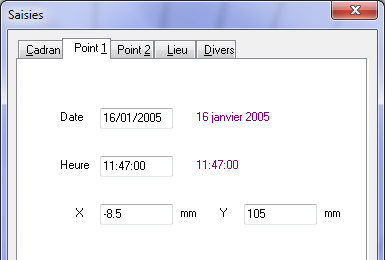
En datant ainsi les instants \(t_1 = j_1 + H_1\) et \(t_2 = j_2 + H_2\) de chaque mesure, nous pouvons en déduire, à l’aide d’éphémérides calculées, les grandeurs suivantes (
11) :
- les déclinaisons \(d_1\) et \(d_2\) du Soleil
- les équations du temps \(E_1\) et \(E_2\) qui permettent de calculer d’après la formule :
\(A = 15°\cdot (H_1 – E_1 – H_2 + E_2)\)
l’angle \(A\) qui correspond à l’angle horaire orienté (\(A\) peut être négatif si, par exemple, \(H_1 > H_2\) avec \(j_1 = j_2\)) entre les positions du Soleil aux instants \(t_1\) et \(t_2\).
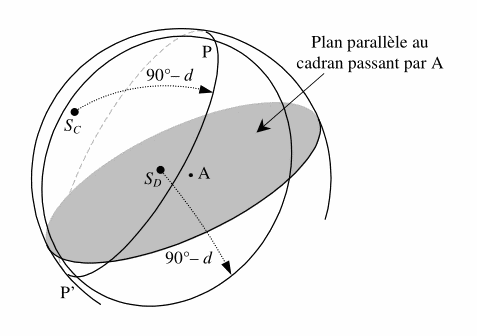
Avec les angles \(d_1\), \(d_2\) et \(A\), on peut définir un triangle sphérique aux sommets duquel se trouvent le pôle nord \(N\) et les positions calculées du Soleil \(S’_1\) et \(S’_2\) aux instants \(t_1\) et \(t_2\) comme le montre la figure suivante. Le sens horaire de l’angle \(A\) définit le triangle de façon unique.
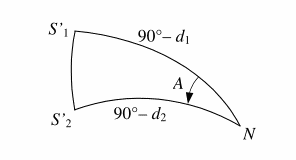
Nous avons par ailleurs, avec les 2 points d’ombre, les positions du Soleil \(S_1\) et \(S_2\) sur la demi-sphère céleste qui est vue par le cadran. Il suffit donc de positionner le triangle précédent en faisant coïncider les sommets \(S’_1\) et \(S’_2\) avec les positions \(S_1\) et \(S_2\) pour trouver la place exacte et unique du pôle nord \(N\) sur la sphère et par suite dans le repère du cadran.
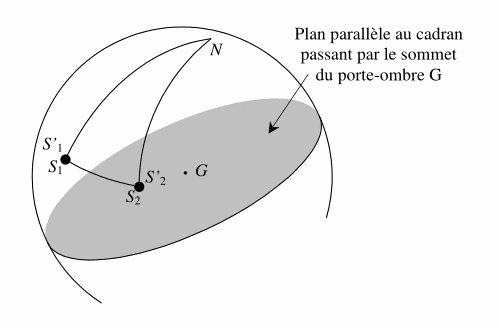
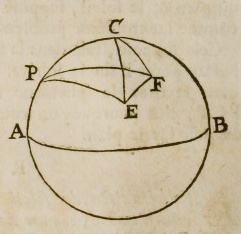
En fait, les couples de points \((S_1, S_2)\) et \((S’_1, S’_2)\) n’étant pas obtenus de la même manière, les imperfections de mesure feront que les points ne coïncideront pas exactement. Le principe retenu dans Calcad pour mettre en place le triangle \(S’_1NS’_2\) est de placer l’arc \(S’_1S’_2\) sur le même grand cercle que celui passant par \(S_1S_2\) et de telle façon que les angles \(S_1S’_1\) et \(S_2S’_2\) soient identiques comme indiqué sur la figure suivante.
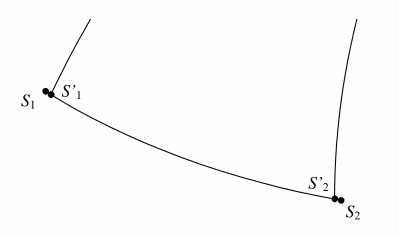
D’autre part, la valeur absolue de la différence des angles \(S_1S_2\) et \(S’_1S’_2\) fournira un indicateur qui confirmera que la méthode à été appliquée sans erreur si le résultat obtenu est proche de 0. Cette valeur, convertie en minute de temps, est l’« indice de précision » fourni par Calcad.
Enfin, pour mettre en place l’éventail des lignes horaires, le principe qui a été retenu est de considérer les dates et heures saisies comme les grandeurs les plus fiables. C’est donc la position \(S’_1\) qui sera considérée comme la position exacte du Soleil à l’heure \(H_1\). Connaissant par ailleurs l’équation du temps \(E_1\) et la position de l’axe polaire, il est très facile de retrouver la position du soleil moyen à l’heure \(H_1\), d’en déduire sa position pour toutes les heures et, par projection, obtenir toutes les lignes horaires correspondantes. Ces lignes sont celles tracées sur les cadrans modernes auxquelles il suffit d’ajouter l’équation du temps et éventuellement tenir compte du changement d’heure été/hiver pour obtenir l’heure civile.
Reste maintenant la mise en pratique de la méthode, c’est-à-dire la mesure des 2 points d’ombre et le report des lignes calculées sur le cadran. Pour limiter les outillages spécifiques – Calcad s’adresse à ceux qui n’ont jamais construit de cadran – il a été choisi d’effectuer la mesure directement sur le plan du cadran. Pour cela, la place privilégiée du système d’axe est le centre de la surface disponible, la position des points d’ombre n’étant pas connue apriori. On peut en profiter pour tracer alors le contour du cadran, nous disposons ainsi d’un cadre sur lequel nous pourrons définir la position des lignes à longueur indéfinie comme le sont habituellement les lignes horaires.
Les premières lignes à tracer sont donc celle d’un carré ou d’un rectangle dont les dimensions seront renseignées. Du milieu de chaque coté \(X\), \(X’\), \(Y\) et \(Y’\) le système d’axe est tracé et le point origine \(O\) déterminé. Il faut ensuite mettre en place le gnomon outil de pied \(O\) et de hauteur à renseigner.
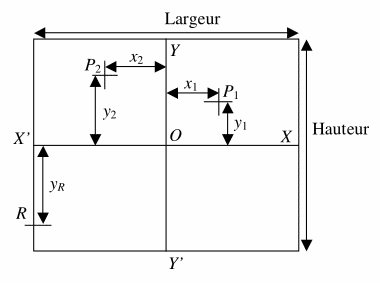
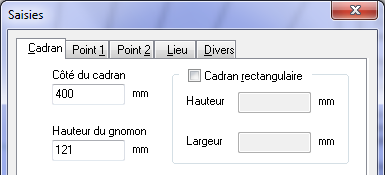
Les positions des 2 points d’ombre, \(P_1\) et \(P_2\), sont alors saisies par leurs coordonnées \((x_1, y_1)\) et \((x_2, y_2)\). En rajoutant l’heure et la date pour chaque point, nous avons ainsi
toutes les valeurs nécessaires pour définir entièrement le cadran.
La vue d’écran suivante illustre la façon dont Calcad présente les résultats : un graphique associé à une zone de texte donnant, en plus des résultats chiffrés, quelques indications concernant le type de cadran.
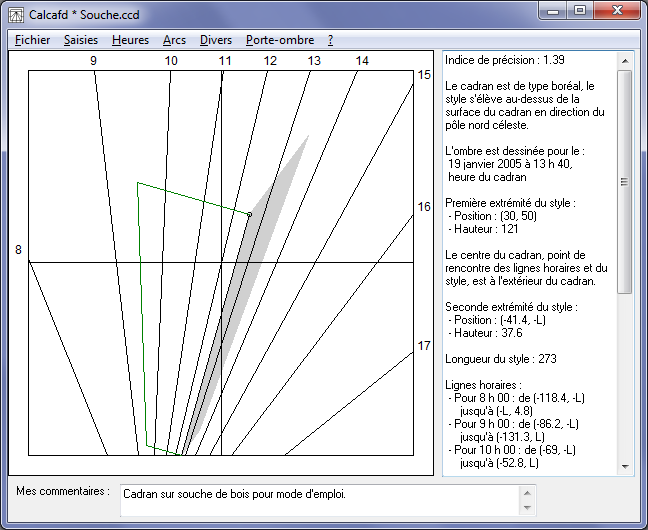
Les points résultats, qui permettent de tracer les lignes du cadran et placer le style, sont indiqués par leurs coordonnées. Toutefois, quand les points sont situés sur le pourtour du cadran (comme le point \(R\) de la figure précédente), ils ne sont définis que par une seule coordonnée, le signe de la seconde coordonnée sera associé à la lettre \(L\) pour indiquer que le point se situe sur la \(L\)imite extérieure. Le style est défini par ses deux extrémités, chaque extrémité par sa position et sa hauteur. Dans le cas d’un cadran à centre, la hauteur du coté du centre n’est pas précisée car par définition elle est nulle.
Dans le principe que nous venons de voir, nous n’avons à aucun moment fait référence à l’horizon ce qui a deux conséquences importantes. La première, qui est surprenante quand on à l’habitude d’utiliser les méthodes classiques de la gnomonique, c’est qu’il n’y a aucune contrainte sur la façon de tracer le repère par rapport à l’horizon. Il peut être incliné sans que cela n’apporte aucun changement dans le mode opératoire.
La seconde est que, parmi les lignes horaires calculées, certaines correspondent à des heures de nuit et ne seront donc pas utiles. Pour que Calcad ne fournisse que les lignes horaires nécessaires, il est prévu plusieurs niveaux, en fonction des informations connues de l’utilisateur, pour introduire la position de l’horizon (
12). Celle-ci sera entièrement définie par la connaissance du zénith que Calcad place sur la sphère au-dessus du cadran dont il connaît la position du pôle nord et des cercles horaires.
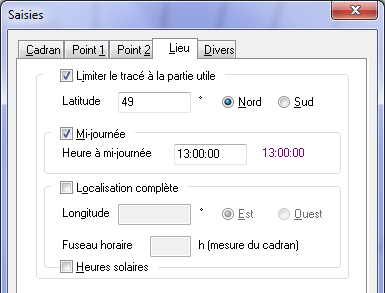
La première donnée nécessaire est la distance entre le pôle nord et le zénith, elle est obtenue par la saisie de la latitude du lieu. Avec cette seule donnée, Calcad considère que le zénith se situe sur le cercle de 12 heures. L’utilisateur peut cependant préciser ce cercle horaire en donnant soit l’heure du milieu de la journée soit la longitude et le fuseau horaire. Dans ce dernier cas, Calcad prendra en compte le fuseau horaire dans le calcul des éphémérides pour augmenter leur précision.
La position de l’horizon permet aussi d’effectuer la correction de la réfraction. Bien qu’elle soit généralement calculée dans le repère local, sa prise en compte directement dans le repère du cadran se fait sans grande complexité comme on le constatera dans la démonstration suivante qui donne les formules utilisées par Calcad.
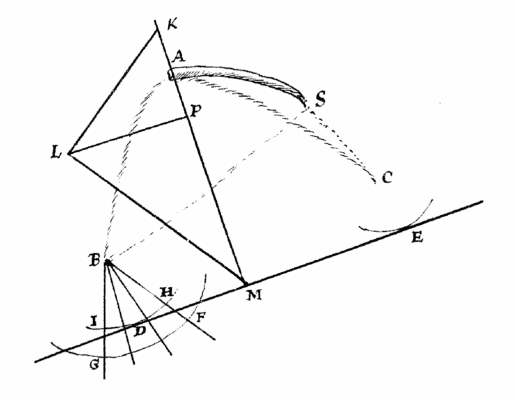
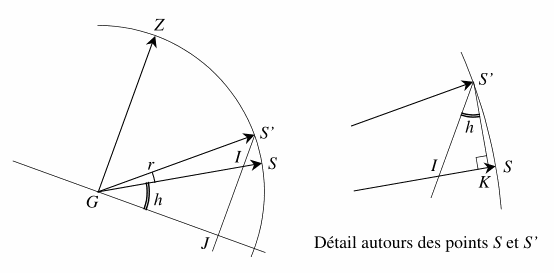
Sur la figure suivante, en se plaçant dans le plan contenant l’extrémité du gnomon, le zénith et le Soleil (pour un observateur c’est un plan vertical mais dans le repère du cadran c’est un plan quelconque), on peut tracer les vecteurs \(\overrightarrow{GZ}\) et \(\overrightarrow{GS}\) pointant respectivement vers le zénith et le Soleil. La position du Soleil apparent, conséquence de la réfraction atmosphérique, sera pointée par le vecteur \(\overrightarrow{GS’}\) qui se trouve aussi dans le plan de la figure.
Les vecteurs \(\overrightarrow{GZ}\) et \(\overrightarrow{GS}\) utilisés par Calcad sont des vecteurs unitaires, on peut donc calculer l’angle \(h\) de la hauteur du Soleil sur l’horizon en utilisant le produit scalaire :
\(\overrightarrow{GZ}\cdot\overrightarrow{GS} = x_Z\cdot x_S + y_Z\cdot y_S + z_Z\cdot z_Z = \cos(90°- h) = \sin h\)
De \(h\), la loi de la réfraction nous donne la valeur de la réfraction atmosphérique \(r\). Le vecteur \(\overrightarrow{GS’}\) cherché peut se décomposer de la façon suivante :
\(\overrightarrow{GS’} = \overrightarrow{GI} + \overrightarrow{IS’}\)
\(\overrightarrow{GS’} = m\cdot\overrightarrow{GS} + n\cdot\overrightarrow{GZ}\)
\(m\) et \(n\) sont des valeurs inférieures à 1, elles sont obtenues par les relations suivantes :
\(m = \frac{GJ}{\cos h} = \frac{\cos (h + r)}{\cos h}\)
et d’après le détail autours des points \(S\) et \(S'\) :
\(n = \frac{S’K}{\cos h} = \frac{\sin r}{\cos h}\)
Calcad fonctionne sur Windows, Linux et Mac OS X, il dispose aussi de fonctionnalités avancées parmi lesquelles on peut notamment citer :
- Configuration des lignes à tracer dont les courbes en demi-huit et les arcs diurnes
- Modification de la position et de la grandeur du style de façon interactive
- Sauvegarde / impression des données et du graphique
- Visualisation et animation de l’ombre
- Définition d’un cadran suivant la méthode classique (inclinaison / déclinaison)
- Export du tracé au format dxf
- Aide contextuelle complète avec manuel d’utilisation
- Calculs spécifiques pour gnomonistes avertis avec le raccourci clavier Ctrl+Y et en fonction des valeurs de la boîte de saisie (cette fonction n’est pas documentée, elle donne essentiellement les valeurs des éphémérides calculées et la mesure de l’orientation d’un plan par un seul point d'ombre)
Cet exposé ce termine ici. Je vous laisse le soin de découvrir par vous-même toutes les possibilités de Calcad. Bien sûr, si certains points ne vous semblent pas évidents, n’hésitez pas à demander des éclaircissements.
11
^ - Un calcul précis demande la connaissance du temps universel qui ne peut être déterminé qu’avec la valeur du fuseau horaire. L’absence de cette valeur permet toutefois d’obtenir une précision acceptable, l’erreur la plus importante provenant du calcul des déclinaisons aux équinoxes pour les pays éloignés du méridien de Greenwich. Elle n’excède pas 1/4 de degré sur la position du pôle nord ce qui se traduit par une erreur d’environ 1/2 minute à la lecture du cadran.
12
^ - L’horizon étant facultatif, il n’est pas nécessaire de définir sa position avec précision.