Mesure de la déclinaison et de l’inclinaison d’une surface
-
Henri_G
- Messages : 52
- Enregistré le : dim. 11 nov. 2018 19:39
- Localisation : Saint-Etienne
- Contact :
Re: Mesure de la déclinaison et de l’inclinaison d’une surface
J'ai utilisé un dispositif un peu différent de celui d'Yvon pour mesurer la déclinaison et l'inclinaison d'un cadran. Le principe est toutefois le même.
La photo montre une plaque de médium de 15 mm d'épaisseur (longueur 50 cm et largeur 35 cm) sur laquelle j'ai fixé 4 équerres identiques. L'extrémité du gnomon droit est à l'intersection de deux fils très fins et très tendus. Les deux fils sont à 50 mm de la table (on pourrait faire mieux pour rendre tout à fait négligeable le diamètre des fils).
La plaque a été fixée sur ma table de jardin que j'ai renversée. Elle n'est alors pas tout à fait verticale et un niveau à affichage numérique (pas celui de la photo) affiche une inclinaison vers l'arrière (par rapport à la verticale) de 6,2°.
A partir des mesures de x (suivant la ligne de plus grand pente) et de y (suivant l'horizontale), on peut déterminer l'inclinaison de la plaque et sa déclinaison a priori à un demi degré près si on se donne la peine de faire plusieurs mesures.
La photo montre une plaque de médium de 15 mm d'épaisseur (longueur 50 cm et largeur 35 cm) sur laquelle j'ai fixé 4 équerres identiques. L'extrémité du gnomon droit est à l'intersection de deux fils très fins et très tendus. Les deux fils sont à 50 mm de la table (on pourrait faire mieux pour rendre tout à fait négligeable le diamètre des fils).
La plaque a été fixée sur ma table de jardin que j'ai renversée. Elle n'est alors pas tout à fait verticale et un niveau à affichage numérique (pas celui de la photo) affiche une inclinaison vers l'arrière (par rapport à la verticale) de 6,2°.
A partir des mesures de x (suivant la ligne de plus grand pente) et de y (suivant l'horizontale), on peut déterminer l'inclinaison de la plaque et sa déclinaison a priori à un demi degré près si on se donne la peine de faire plusieurs mesures.
- Yvon_M
- Administrateur du site
- Messages : 402
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Mesure de la déclinaison et de l’inclinaison d’une surface
L’intersection de deux fil est à mon avis une bonne solution. Il me semble aussi que les résultats pourraient être meilleurs avec une hauteur plus grande, au moins du double, car on devrait améliorer la précision relative de cette hauteur et des mesures de x et y.
Une petite question me tenaille : suite à nos échanges au début de ce fil, avez-vous fait des essais autour de midi solaire pour voir si cette méthode se comportait mieux que celle utilisant la longueur de l’ombre ?
Une petite question me tenaille : suite à nos échanges au début de ce fil, avez-vous fait des essais autour de midi solaire pour voir si cette méthode se comportait mieux que celle utilisant la longueur de l’ombre ?
Yvon Massé - Site perso. : La gnomonique
-
Henri_G
- Messages : 52
- Enregistré le : dim. 11 nov. 2018 19:39
- Localisation : Saint-Etienne
- Contact :
Re: Mesure de la déclinaison et de l’inclinaison d’une surface
Il est évident que si on éloigne les fils de la plaque, les résultats ne peuvent être que meilleurs :
1°) L'épaisseur des fils deviendrait vraiment négligeable (quelle est la hauteur du gnomon équivalent : la distance entre la plaque et le bas du fil le plus bas, la distance entre la plaque et le haut du fil le plus bas ou le bas du fil le plus haut, la distance entre la plaque et le haut du fil le plus haut, la distance à la plaque du bas du trou des équerres ?)
2°) L'incertitude sur les mesures de x et y (disons un demi millimètre) relativement à la hauteur de la plaque serait diminuée.
J'ai d'ailleurs des équerres qui permettraient de placer les fils à 87 mm de la plaque.
J'ai voulu montrer les résultats avec les équerres de 50 mm car je les trouve déjà très satisfaisants. Il faut remarquer que je ne me suis pas contenté d'une seule mesure (en fait 8 mesures sur 4h). La méthode est bonne et d'autant meilleure (mais ce n'est que mon avis) qu'on utilise l'application de Mr C. Busto (Gnomonic Photo). En effet cette application fournit l'heure TSV, l'azimut et la hauteur du Soleil (avec, il me semble, compensation de la réfraction atmosphérique) inscrits sur la photo que l'on prend, photo sur laquelle on peut faire la mesure sans toucher au dispositif. Même avec un appareil photo de qualité moyenne sur la tablette, il est facile de repérer sur le papier millimétré où est l'ombre des fils.
Une seule petite restriction à cette méthode est qu'il faut que les fils soient bien tendus, en particulier le fil horizontal qui a tendance à faire ce qu'on appelle la "chaînette" (visualisation de la courbe cosinus hyperbolique des matheux). On s'aperçoit vite de ce défaut si on exploite les résultats au fur et à mesure (ça m'est arrivé).
--------------
La méthode qui utilise la longueur de l'ombre ne convient que pour les murs supposés parfaitement verticaux. Je l'utilisais pour deux raisons (pas forcément très valables) : 1- pas besoin de définir des axes x et y, 2- on n'est pas obligé de trop toucher (heurter) la plaque. Dans mon message précédent où il y a beaucoup de rouge et de vert, je montre qu'il vaut mieux éviter certaines heures ... mais cela peut dépendre aussi de la déclinaison du mur. En fait, quelle que soit la méthode utilisée, je crois qu'il faut (si possible) exploiter les mesures au fur et à mesure. On s'aperçoit vite qu'il y a une trop grande dispersion dans les résultats et là, il faut se poser des questions.
De toute façon, pour un mur parfaitement vertical, j'utiliserai toujours la méthode dite de Schumacher (par Y. Opizzo) avec un déclinomètre à fil.
Par contre pour un mur déclinant incliné, je ne vois pas trop quelle méthode (tout solaire) utiliser autre que celle du gnomon droit avec mesures de x et y. Je fais une confiance tout à fait limitée (peut être à tort) à l'affichage au dixième de degré près d'un niveau numérique.
1°) L'épaisseur des fils deviendrait vraiment négligeable (quelle est la hauteur du gnomon équivalent : la distance entre la plaque et le bas du fil le plus bas, la distance entre la plaque et le haut du fil le plus bas ou le bas du fil le plus haut, la distance entre la plaque et le haut du fil le plus haut, la distance à la plaque du bas du trou des équerres ?)
2°) L'incertitude sur les mesures de x et y (disons un demi millimètre) relativement à la hauteur de la plaque serait diminuée.
J'ai d'ailleurs des équerres qui permettraient de placer les fils à 87 mm de la plaque.
J'ai voulu montrer les résultats avec les équerres de 50 mm car je les trouve déjà très satisfaisants. Il faut remarquer que je ne me suis pas contenté d'une seule mesure (en fait 8 mesures sur 4h). La méthode est bonne et d'autant meilleure (mais ce n'est que mon avis) qu'on utilise l'application de Mr C. Busto (Gnomonic Photo). En effet cette application fournit l'heure TSV, l'azimut et la hauteur du Soleil (avec, il me semble, compensation de la réfraction atmosphérique) inscrits sur la photo que l'on prend, photo sur laquelle on peut faire la mesure sans toucher au dispositif. Même avec un appareil photo de qualité moyenne sur la tablette, il est facile de repérer sur le papier millimétré où est l'ombre des fils.
Une seule petite restriction à cette méthode est qu'il faut que les fils soient bien tendus, en particulier le fil horizontal qui a tendance à faire ce qu'on appelle la "chaînette" (visualisation de la courbe cosinus hyperbolique des matheux). On s'aperçoit vite de ce défaut si on exploite les résultats au fur et à mesure (ça m'est arrivé).
--------------
La méthode qui utilise la longueur de l'ombre ne convient que pour les murs supposés parfaitement verticaux. Je l'utilisais pour deux raisons (pas forcément très valables) : 1- pas besoin de définir des axes x et y, 2- on n'est pas obligé de trop toucher (heurter) la plaque. Dans mon message précédent où il y a beaucoup de rouge et de vert, je montre qu'il vaut mieux éviter certaines heures ... mais cela peut dépendre aussi de la déclinaison du mur. En fait, quelle que soit la méthode utilisée, je crois qu'il faut (si possible) exploiter les mesures au fur et à mesure. On s'aperçoit vite qu'il y a une trop grande dispersion dans les résultats et là, il faut se poser des questions.
De toute façon, pour un mur parfaitement vertical, j'utiliserai toujours la méthode dite de Schumacher (par Y. Opizzo) avec un déclinomètre à fil.
Par contre pour un mur déclinant incliné, je ne vois pas trop quelle méthode (tout solaire) utiliser autre que celle du gnomon droit avec mesures de x et y. Je fais une confiance tout à fait limitée (peut être à tort) à l'affichage au dixième de degré près d'un niveau numérique.
- Yvon_M
- Administrateur du site
- Messages : 402
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Mesure de la déclinaison et de l’inclinaison d’une surface
Merci, Henri, pour cette réponse très complète.
L’utilisation de l’application GnomonicPhoto est effectivement une très bonne idée qui permet de faire les relevés simplement en limitant les risques d’erreur, merci pour ce partage.
J’ai aussi essayé de montrer que, dans ces mêmes conditions, la méthode avec mesure de X et Y ne présentait pas cette restriction. Mais avec des arguments théoriques cela devient vite indigeste et peu convaincant, c’est pourquoi je vous proposais de confirmer cette conjecture par la pratique. Qu’en pensez-vous ?
L’utilisation de l’application GnomonicPhoto est effectivement une très bonne idée qui permet de faire les relevés simplement en limitant les risques d’erreur, merci pour ce partage.
Entièrement d’accord. Pour moi, les instants les plus critiques de cette méthode sont quand l’ombre du gnomon est proche de la verticale, quelque soit la déclinaison du mur.Henri_G a écrit :La méthode qui utilise la longueur de l'ombre ne convient que pour les murs supposés parfaitement verticaux. [...] Dans mon message précédent où il y a beaucoup de rouge et de vert, je montre qu'il vaut mieux éviter certaines heures ... mais cela peut dépendre aussi de la déclinaison du mur.
J’ai aussi essayé de montrer que, dans ces mêmes conditions, la méthode avec mesure de X et Y ne présentait pas cette restriction. Mais avec des arguments théoriques cela devient vite indigeste et peu convaincant, c’est pourquoi je vous proposais de confirmer cette conjecture par la pratique. Qu’en pensez-vous ?
Yvon Massé - Site perso. : La gnomonique
-
Henri_G
- Messages : 52
- Enregistré le : dim. 11 nov. 2018 19:39
- Localisation : Saint-Etienne
- Contact :
Re: Mesure de la déclinaison et de l’inclinaison d’une surface
C'est vrai que les problèmes peuvent se poser quand l'ombre du gnomon est verticale. Il me semble que si on veut le prouver, il vaut mieux une faire démonstration "théorique" plutôt que "pratique" car entachée d'erreurs de mesures. C'est ce que j'ai essayé de faire (le mot "théorique" est un peu pompeux) :
Si on ne s'intéresse qu'aux cadrans verticaux déclinants, il est possible de montrer assez facilement qu'il vaut mieux éviter de faire les mesures quand l'ombre du gnomon est verticale, quelle que soit la méthode, mesure de longueur de l'ombre, mesure de l'angle de l'ombre ou mesure de la coordonnée horizontale du point d'ombre "x" (qui seule suffit pour déterminer la déclinaison du mur). Cela ne veut pas dire que le résultat de la mesure est faux si on la fait à ce moment-là, seulement que la mesure est moins précise qu'à un autre moment. Un peu de calcul différentiel pourrait montrer cela très simplement ..... On va éviter et, c'est mieux, faire deux dessins.
Le premier dessin qui est une vue de dessus montre que lorsque l'ombre du gnomon est verticale, celui-ci est dans le plan contenant le Soleil - en rouge- (à une heure où l'azimut du Soleil est égal à la déclinaison du mur ... et cette heure dépend de la déclinaison du mur et de la date) La valeur de x est zéro. Si à cet instant précis, on pouvait faire pivoter légèrement (disons de 1°) le mur autour d'un axe vertical (c'est à dire changer la déclinaison gnomonique du mur de 1°), la coordonnée horizontale de l'ombre du gnomon varierait d'une quantité égale à L tan(1°), L étant la longueur du gnomon. Si L=100 mm, cela donnerait un déplacement de 1,75 mm. Pour simplifier le dessin, on peut faire tourner le Soleil de 1° par rapport au mur plutôt que le mur de 1° par rapport au Soleil.
Imaginons maintenant que l'on fasse la mesure à un autre instant. Le gnomon et son ombre sont schématisés sur le deuxième dessin. La valeur de x est différente de zéro. Imaginons encore qu'à ce moment là on fasse pivoter le mur de 1°. On voit tout de suite que le point d'ombre se déplace beaucoup plus que précédemment. On peut encore faire un petit calcul. Si à l'heure de cette deuxième mesure, l'angle "alpha" (voir dessin, alpha est l'azimut du Soleil moins la déclinaison du mur) vaut 50°, la coordonnée horizontale du point d'ombre est x = L tan(50°)= 119,2 mm. Si on faisait pivoter le mur de 1°, cette valeur deviendrait L tan(51°)= 123,5 mm. Le déplacement est supérieur à 4 mm.
La précision de la mesure peut être chiffrée par le rapport (variation de x) divisée par (variation de la déclinaison). Plus le rapport est grand, plus la mesure est précise. Quand l'ombre est verticale (alpha =0°) le rapport vaut 1,75 mm par degré.
A l'autre moment considéré (alpha = 50°), le rapport vaut 4 mm par degré... c'est à dire que 1,75 mm ne correspondront pas à 1° mais à 1,75/4= 0,45°. La mesure sera donc plus précise.
Si on ne s'intéresse qu'aux cadrans verticaux déclinants, il est possible de montrer assez facilement qu'il vaut mieux éviter de faire les mesures quand l'ombre du gnomon est verticale, quelle que soit la méthode, mesure de longueur de l'ombre, mesure de l'angle de l'ombre ou mesure de la coordonnée horizontale du point d'ombre "x" (qui seule suffit pour déterminer la déclinaison du mur). Cela ne veut pas dire que le résultat de la mesure est faux si on la fait à ce moment-là, seulement que la mesure est moins précise qu'à un autre moment. Un peu de calcul différentiel pourrait montrer cela très simplement ..... On va éviter et, c'est mieux, faire deux dessins.
Le premier dessin qui est une vue de dessus montre que lorsque l'ombre du gnomon est verticale, celui-ci est dans le plan contenant le Soleil - en rouge- (à une heure où l'azimut du Soleil est égal à la déclinaison du mur ... et cette heure dépend de la déclinaison du mur et de la date) La valeur de x est zéro. Si à cet instant précis, on pouvait faire pivoter légèrement (disons de 1°) le mur autour d'un axe vertical (c'est à dire changer la déclinaison gnomonique du mur de 1°), la coordonnée horizontale de l'ombre du gnomon varierait d'une quantité égale à L tan(1°), L étant la longueur du gnomon. Si L=100 mm, cela donnerait un déplacement de 1,75 mm. Pour simplifier le dessin, on peut faire tourner le Soleil de 1° par rapport au mur plutôt que le mur de 1° par rapport au Soleil.
Imaginons maintenant que l'on fasse la mesure à un autre instant. Le gnomon et son ombre sont schématisés sur le deuxième dessin. La valeur de x est différente de zéro. Imaginons encore qu'à ce moment là on fasse pivoter le mur de 1°. On voit tout de suite que le point d'ombre se déplace beaucoup plus que précédemment. On peut encore faire un petit calcul. Si à l'heure de cette deuxième mesure, l'angle "alpha" (voir dessin, alpha est l'azimut du Soleil moins la déclinaison du mur) vaut 50°, la coordonnée horizontale du point d'ombre est x = L tan(50°)= 119,2 mm. Si on faisait pivoter le mur de 1°, cette valeur deviendrait L tan(51°)= 123,5 mm. Le déplacement est supérieur à 4 mm.
La précision de la mesure peut être chiffrée par le rapport (variation de x) divisée par (variation de la déclinaison). Plus le rapport est grand, plus la mesure est précise. Quand l'ombre est verticale (alpha =0°) le rapport vaut 1,75 mm par degré.
A l'autre moment considéré (alpha = 50°), le rapport vaut 4 mm par degré... c'est à dire que 1,75 mm ne correspondront pas à 1° mais à 1,75/4= 0,45°. La mesure sera donc plus précise.
- Yvon_M
- Administrateur du site
- Messages : 402
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Mesure de la déclinaison et de l’inclinaison d’une surface
Merci beaucoup, Henri, pour ces explications très détaillées. Je suis entièrement d’accord avec vous sur le critère que vous avez retenu pour évaluer la précision de la mesure. Je ne suis pas sûr qu’il soit suffisant, mais il est au moins nécessaire et, de plus, facile à évaluer.
Par contre, là où je ne suis absolument pas d’accord, c’est de loger toutes les méthodes à la même enseigne :
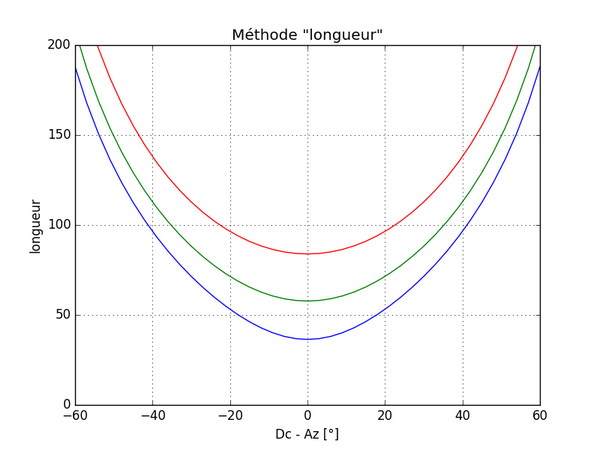
On remarque qu’effectivement la méthode « longueur » est véritablement « nulle », comme sa dérivée, quand le Soleil est juste en face du mur, ou encore quand l’ombre est verticale.
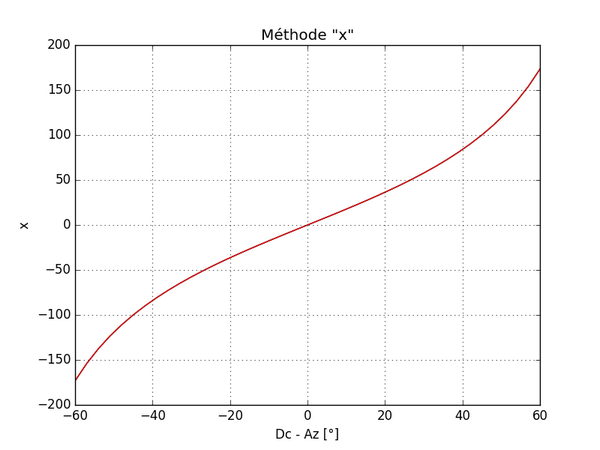
La méthode « x », que vous avez commentée, ne dépend pas de la hauteur du Soleil (les 3 courbes sont superposées). Elle est effectivement moins « sensible » quand l’ombre est verticale, mais cela n’a rien de comparable avec la méthode « longueur ».
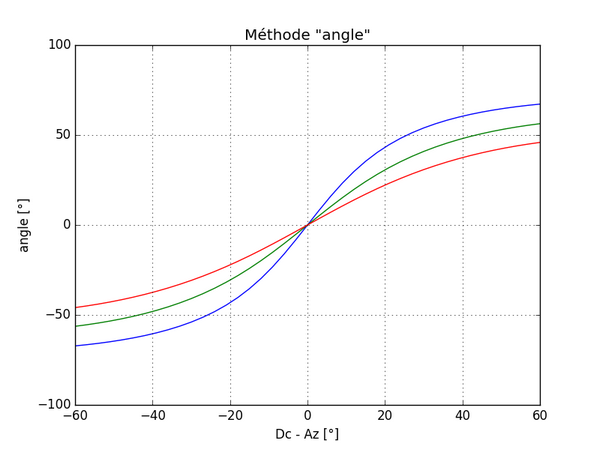
Quant à la méthode « angle », c’est justement quand l’ombre est verticale qu’elle est la plus « sensible ». Elle l’est d’autant plus que le Soleil est bas sur l’horizon.
Pour résumer, s’il y a un méthode à bannir, notamment quand l’ombre du gnomon est verticale, c’est uniquement la méthode « longueur ».
Par contre, là où je ne suis absolument pas d’accord, c’est de loger toutes les méthodes à la même enseigne :
Pour vous convaincre du contraire, je reprendrai votre critère et, pour éviter aussi le calcul des dérivées, je vous propose de les apprécier sur les courbes qui suivent. Elles donnent les valeurs mesurées en fonction de la différence : déclinaison gnomonique – azimut du Soleil. Enfin, pour être plus général, j’ai tracé ces courbes pour 3 hauteurs différentes du Soleil : 20° (en bleu), 40° (en vert) et 60° (en rouge).Henri_G a écrit :[…] il vaut mieux éviter de faire les mesures quand l'ombre du gnomon est verticale, quelle que soit la méthode, mesure de longueur de l'ombre, mesure de l'angle de l'ombre ou mesure de la coordonnée horizontale du point d'ombre "x" (qui seule suffit pour déterminer la déclinaison du mur) […]
On remarque qu’effectivement la méthode « longueur » est véritablement « nulle », comme sa dérivée, quand le Soleil est juste en face du mur, ou encore quand l’ombre est verticale.

La méthode « x », que vous avez commentée, ne dépend pas de la hauteur du Soleil (les 3 courbes sont superposées). Elle est effectivement moins « sensible » quand l’ombre est verticale, mais cela n’a rien de comparable avec la méthode « longueur ».

Quant à la méthode « angle », c’est justement quand l’ombre est verticale qu’elle est la plus « sensible ». Elle l’est d’autant plus que le Soleil est bas sur l’horizon.

Pour résumer, s’il y a un méthode à bannir, notamment quand l’ombre du gnomon est verticale, c’est uniquement la méthode « longueur ».
Yvon Massé - Site perso. : La gnomonique
-
Henri_G
- Messages : 52
- Enregistré le : dim. 11 nov. 2018 19:39
- Localisation : Saint-Etienne
- Contact :
Re: Mesure de la déclinaison et de l’inclinaison d’une surface
C'est sûr que "x" varie le plus avec Dc-Az.
Vos courbes m'expliquent bien pourquoi certaines mesures que j'ai faites avec la longueur de l'ombre, quand celle-ci était verticale, ne m'ont pas donné de bons résultats. Elles m'expliquent aussi pourquoi, quand Dc-Az est "grand", elle m'a donné des résultats corrects.
Elles montrent aussi (sauf pour la mesure de l'angle***) qu'il vaut mieux éviter de faire les mesures quand Dc-Az est faible (ombre verticale)... même si avec "x" on peut obtenir des résultats très corrects (en plus c'est la méthode dont les résultats sont le plus faciles à exploiter .. un "simple" arctangente quand le mur est tout à fait vertical). Pour s'en convaincre, il suffit de regarder le tableau des mesures que j'ai faites sur ma table de jardin (pas tout à fait verticale - voir post précédent) où autour de 14.597h, la valeur de "y" (qui est ici notre "x") est, en valeur absolue, la pus faible (ombre presque verticale). Les résultats obtenus pour "theta" et "D" sont tout à fait compatibles avec les résultats des autres mesures.
*** La mesure de l'angle semble donner de meilleurs résultats l'hiver, quand l'ombre verticale est courte ... mais uniquement pendant l'hiver et pendant peu de temps dans la journée. quant à la mesure d'un angle .... quelle précision ?
En définitive, il vaut mieux utiliser la méthode "x" (quand le mur est vertical) et de préférence quand l'ombre n'est pas verticale.
[Suggestion : Yvon pourrait nous tracer la dérivée de sa courbe x en fonction de Dc-Az, c'est à dire (variation de x)/(variation de Dc-Az) ?]
Quand le mur est pas vertical et incliné, la seule méthode qui existe (à ma connaissance) est la méthode "x" et "y" ... donc c'est la meilleure.
Vos courbes m'expliquent bien pourquoi certaines mesures que j'ai faites avec la longueur de l'ombre, quand celle-ci était verticale, ne m'ont pas donné de bons résultats. Elles m'expliquent aussi pourquoi, quand Dc-Az est "grand", elle m'a donné des résultats corrects.
Elles montrent aussi (sauf pour la mesure de l'angle***) qu'il vaut mieux éviter de faire les mesures quand Dc-Az est faible (ombre verticale)... même si avec "x" on peut obtenir des résultats très corrects (en plus c'est la méthode dont les résultats sont le plus faciles à exploiter .. un "simple" arctangente quand le mur est tout à fait vertical). Pour s'en convaincre, il suffit de regarder le tableau des mesures que j'ai faites sur ma table de jardin (pas tout à fait verticale - voir post précédent) où autour de 14.597h, la valeur de "y" (qui est ici notre "x") est, en valeur absolue, la pus faible (ombre presque verticale). Les résultats obtenus pour "theta" et "D" sont tout à fait compatibles avec les résultats des autres mesures.
*** La mesure de l'angle semble donner de meilleurs résultats l'hiver, quand l'ombre verticale est courte ... mais uniquement pendant l'hiver et pendant peu de temps dans la journée. quant à la mesure d'un angle .... quelle précision ?
En définitive, il vaut mieux utiliser la méthode "x" (quand le mur est vertical) et de préférence quand l'ombre n'est pas verticale.
[Suggestion : Yvon pourrait nous tracer la dérivée de sa courbe x en fonction de Dc-Az, c'est à dire (variation de x)/(variation de Dc-Az) ?]
Quand le mur est pas vertical et incliné, la seule méthode qui existe (à ma connaissance) est la méthode "x" et "y" ... donc c'est la meilleure.
- Yvon_M
- Administrateur du site
- Messages : 402
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Mesure de la déclinaison et de l’inclinaison d’une surface
Comme vous l’avez fait remarquer, la fonction "x" = f(Dc-Az) est du type tangente, sa dérivée est donc du type 1/cos²(Dc-Az).Henri_G a écrit :Suggestion : Yvon pourrait nous tracer la dérivée de sa courbe x en fonction de Dc-Az, c'est à dire (variation de x)/(variation de Dc-Az) ?
Pour que cette fonction dérivée soit à utilisation pratique, je l’ai exprimée en %/°. Le pourcentage étant la variation de la grandeur "x" ramenée à la longueur du gnomon. Voici donc sa courbe :
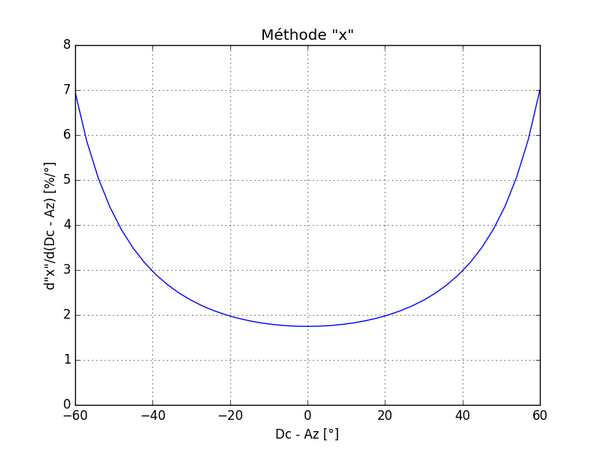
Ainsi, si la différence Dc-Az est de 20°, "x" variera de 2 mm pour un gnomon de 100 mm quand Dc-Az variera d’1°.
Pour revenir à la méthode "x" et "y" dans le cas d’un mur vertical, on peut remarquer qu’elle s’apparente dans ce cas à la méthode « angle » car celui-ci s’obtient directement avec "x" et "y". Même si la hauteur du Soleil est importante, elle fonctionne aussi bien pour toutes les valeur de Dc-Az. Pourrait-on dire alors qu’elle a toutes les qualités d’une méthode universelle ?
Yvon Massé - Site perso. : La gnomonique
-
Henri_G
- Messages : 52
- Enregistré le : dim. 11 nov. 2018 19:39
- Localisation : Saint-Etienne
- Contact :
Re: Mesure de la déclinaison et de l’inclinaison d’une surface
Merci pour cette courbe. On y retrouve les valeurs que j'avais indiquées : 1,75 mm pour Dc-Az=0° et 4 mm pour Dc-Az=50°.... et même plus si on fait la mesure en été avec Dc-Az encore plus grand.
Merci aussi pour ces échanges qui m'ont convaincu de l'intérêt de la méthode "x" (je vais remplacer les petites équerres de mon dispositif par de plus grandes). J'ai abandonné la mesure de la longueur de l'ombre depuis longtemps.
Enfin une question que je me pose maintenant :
Parmi les deux méthodes qui permettent de déterminer la déclinaison d'un mur vertical par la mesure de Dc-Az, directe (avec le déclinomètre à fil de Schumacher) ou indirecte (méthode "x" - par tangente(Dc-Az)), quelle est la meilleure ? d'un point de vue "théorique" ? d'un point de vue pratique ?
"théorique" : si on définit la sensibilité de la méthode par : variation de la mesure avec une variation de la déclinaison Dc
Avec le déclinomètre à fil, c'est un degré de mesure pour un degré de déclinaison quelle que soit la saison (il faut donc avoir un bon rapporteur)
Avec la méthode "x", la sensibilité est variable comme le montre la courbe de Yvon dans un rapport de 1 à 3 presque 4)
"expérimental" : pour avoir les deux dispositifs, le déclinomètre à fil est indéréglable alors que les fils sur la plaque peuvent se détendre ; par contre la mesure de "x" ne demande aucune intervention de l'opérateur si on prend une photo .... alors ?
Alors ... on doit pouvoir discuter pendant des heures.
Je vais essayer de tester les deux ... en me servant de l'application Gnomonic Photo .... à suivre !
Merci aussi pour ces échanges qui m'ont convaincu de l'intérêt de la méthode "x" (je vais remplacer les petites équerres de mon dispositif par de plus grandes). J'ai abandonné la mesure de la longueur de l'ombre depuis longtemps.
Enfin une question que je me pose maintenant :
Parmi les deux méthodes qui permettent de déterminer la déclinaison d'un mur vertical par la mesure de Dc-Az, directe (avec le déclinomètre à fil de Schumacher) ou indirecte (méthode "x" - par tangente(Dc-Az)), quelle est la meilleure ? d'un point de vue "théorique" ? d'un point de vue pratique ?
"théorique" : si on définit la sensibilité de la méthode par : variation de la mesure avec une variation de la déclinaison Dc
Avec le déclinomètre à fil, c'est un degré de mesure pour un degré de déclinaison quelle que soit la saison (il faut donc avoir un bon rapporteur)
Avec la méthode "x", la sensibilité est variable comme le montre la courbe de Yvon dans un rapport de 1 à 3 presque 4)
"expérimental" : pour avoir les deux dispositifs, le déclinomètre à fil est indéréglable alors que les fils sur la plaque peuvent se détendre ; par contre la mesure de "x" ne demande aucune intervention de l'opérateur si on prend une photo .... alors ?
Alors ... on doit pouvoir discuter pendant des heures.
Je vais essayer de tester les deux ... en me servant de l'application Gnomonic Photo .... à suivre !
Re: Mesure de la déclinaison et de l’inclinaison d’une surface
Une autre méthode très employée parmi nous, celle "des bissectrices" - "de l'hyperbole". C'est la même.
Elle est simple, pratique, fiable, précise, et pas besoin d'informatique.
Il suffit d'un petit outillage facile à réaliser, et un enfant peut s'avérer très motivé pour effectuer les relevés.
Je peux développer la procédure pour ceux qui pourraient être intéressés.
Elle est simple, pratique, fiable, précise, et pas besoin d'informatique.
Il suffit d'un petit outillage facile à réaliser, et un enfant peut s'avérer très motivé pour effectuer les relevés.
Je peux développer la procédure pour ceux qui pourraient être intéressés.