Énigme gnomonique
- Yvon_M
- Administrateur du site
- Messages : 411
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Énigme gnomonique
Pour nous dérouiller en vue de cette rentrée 2019, je vous propose une petite énigme gnomonique.
Nous avons tous vu, avec un petit sourire, ces cadrans naïfs réalisés par des bricoleurs maladroits où le style est planté perpendiculairement au mur. En effet, nous savons pertinemment que ce type de cadran ne peut indiquer correctement les heures solaires au cours d’une année.
J’ai toutefois décidé de relever ce défi et d’installer sur le mur vertical de mon domicile, situé à la latitude de 49° nord et déclinant de 71° à l’ouest, un style rectiligne horizontal qui m’indique correctement l’heure solaire sur une droite graduée. Bien sûr, il n’y a pas de miracle : je dois déplacer ce style au cours des saisons mais je n’effectue qu’une simple translation.
Pourriez-vous m’indiquer quelle astuce j’ai utilisée et décrire, ou mieux dessiner, le cadran que j’ai conçu ?
Nous avons tous vu, avec un petit sourire, ces cadrans naïfs réalisés par des bricoleurs maladroits où le style est planté perpendiculairement au mur. En effet, nous savons pertinemment que ce type de cadran ne peut indiquer correctement les heures solaires au cours d’une année.
J’ai toutefois décidé de relever ce défi et d’installer sur le mur vertical de mon domicile, situé à la latitude de 49° nord et déclinant de 71° à l’ouest, un style rectiligne horizontal qui m’indique correctement l’heure solaire sur une droite graduée. Bien sûr, il n’y a pas de miracle : je dois déplacer ce style au cours des saisons mais je n’effectue qu’une simple translation.
Pourriez-vous m’indiquer quelle astuce j’ai utilisée et décrire, ou mieux dessiner, le cadran que j’ai conçu ?
Yvon Massé - Site perso. : La gnomonique
-
Stéphane_L
- Messages : 111
- Enregistré le : lun. 3 juin 2019 21:33
Re: Énigme gnomonique
Pour lire l’heure sur le cadran, y a-t-il une ou plusieurs droites graduées ?
- Yvon_M
- Administrateur du site
- Messages : 411
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Énigme gnomonique
Il n'y a qu'une seule droite horaire, Stéphane. Il y a aussi des repères pour placer le style suivant la date. C'est l'ombre rectiligne du style qui donne l'heure sur la droite horaire.
Tous mes encouragements pour ta recherche de la solution.
Tous mes encouragements pour ta recherche de la solution.
Yvon Massé - Site perso. : La gnomonique
-
Stéphane_L
- Messages : 111
- Enregistré le : lun. 3 juin 2019 21:33
Re: Énigme gnomonique
Les graduations horaires de la droite peuvent-elles varier en fonction de la date (par un système mécanique lié au pied du style) ?
- Yvon_M
- Administrateur du site
- Messages : 411
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Énigme gnomonique
Non, Stéphane, les graduations horaires sont fixes.
Allez, je donne quelques indices : le cadran que j’ai conçu appartient à une famille particulière de cadran qu’on rencontre de plus en plus fréquemment. Un mathématicien peu connu a présenté à l’Académie royale des sciences, au tout début du 18e siècle, une configuration proche de celle que j’ai utilisée.
La clef de l’énigme ne devrait maintenant plus poser de problème .
.
Allez, je donne quelques indices : le cadran que j’ai conçu appartient à une famille particulière de cadran qu’on rencontre de plus en plus fréquemment. Un mathématicien peu connu a présenté à l’Académie royale des sciences, au tout début du 18e siècle, une configuration proche de celle que j’ai utilisée.
La clef de l’énigme ne devrait maintenant plus poser de problème
Yvon Massé - Site perso. : La gnomonique
-
Stéphane_L
- Messages : 111
- Enregistré le : lun. 3 juin 2019 21:33
Re: Énigme gnomonique
Merci pour l'info.
À partir du cadran analemmatique universel d'Antoine Parent, voici ma proposition. Le style est bien horizontal rectiligne (mais pas perpendiculaire au plan) et la droite graduée n'est pas dans le plan du cadran.

À partir du cadran analemmatique universel d'Antoine Parent, voici ma proposition. Le style est bien horizontal rectiligne (mais pas perpendiculaire au plan) et la droite graduée n'est pas dans le plan du cadran.
- Fichiers joints
-
- cadran.png (134.83 Kio) Vu 95510 fois
- Yvon_M
- Administrateur du site
- Messages : 411
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Énigme gnomonique
Félicitations Stéphane, c’est bien la référence à Antoine Parent que je proposais comme indice.
Votre proposition est tout à fait fonctionnelle mais ce n’est pas exactement le cadran que j’avais imaginé. En effet, comme vous le proposez, on peut utiliser une verge graduée placée dans le plan du méridien pour lire l’heure mais ce n’est pas le plus simple ni le plus facile à lire. On peut tout simplement, et dans l’esprit du cadran analemmatique, utiliser la projection de cette verge (ou de façon plus générale la projection du cercle horaire équatorial) sur le plan du cadran suivant la direction du style.
Je ferai aussi 2 remarques concernant votre proposition. Sauf erreur, il me semble que les proportions entre la ligne des dates et la droite horaire ne sont pas respectées : pour moi, la ligne des dates devrait être plus longue. Enfin, mais ce n’est qu’un détail, l’énigme concernait un mur déclinant de 71° alors que le cadran que vous proposez correspond à une déclinaison de 61°.
Voici donc le cadran que je voulais faire deviner. Comme le précise Stéphane avec justesse, le style est horizontal mais n’est pas perpendiculaire au mur : il est rigoureusement dirigé vers l’ouest.
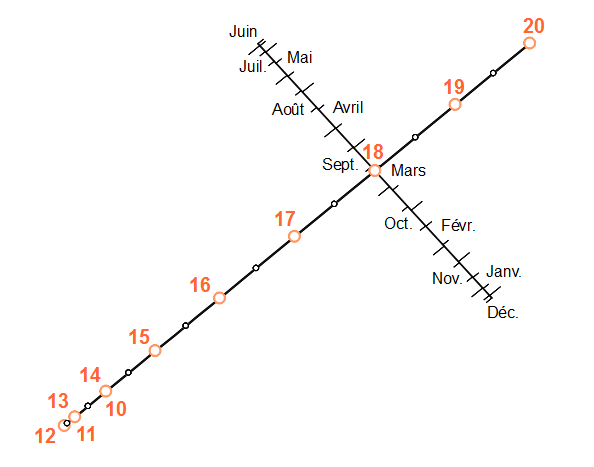
Bien que cela n’apparaisse pas de façon sensible, il faut noter que les droites des heures et des dates ne sont pas perpendiculaires. Elles le deviennent dans le cas du cadran de Parent ci-dessous où le plan est celui du méridien, soit une déclinaison correspondante de 90°.
Bien sûr, j’aurais aussi pu choisir un style perpendiculaire au mur. Dans ce cas la droite horaire aurait pris la forme elliptique classique du cadran analemmatique comme on peut le voir ci-dessous.
Encore bravo Stéphane pour votre ténacité à chercher la solution.
Votre proposition est tout à fait fonctionnelle mais ce n’est pas exactement le cadran que j’avais imaginé. En effet, comme vous le proposez, on peut utiliser une verge graduée placée dans le plan du méridien pour lire l’heure mais ce n’est pas le plus simple ni le plus facile à lire. On peut tout simplement, et dans l’esprit du cadran analemmatique, utiliser la projection de cette verge (ou de façon plus générale la projection du cercle horaire équatorial) sur le plan du cadran suivant la direction du style.
Je ferai aussi 2 remarques concernant votre proposition. Sauf erreur, il me semble que les proportions entre la ligne des dates et la droite horaire ne sont pas respectées : pour moi, la ligne des dates devrait être plus longue. Enfin, mais ce n’est qu’un détail, l’énigme concernait un mur déclinant de 71° alors que le cadran que vous proposez correspond à une déclinaison de 61°.
Voici donc le cadran que je voulais faire deviner. Comme le précise Stéphane avec justesse, le style est horizontal mais n’est pas perpendiculaire au mur : il est rigoureusement dirigé vers l’ouest.

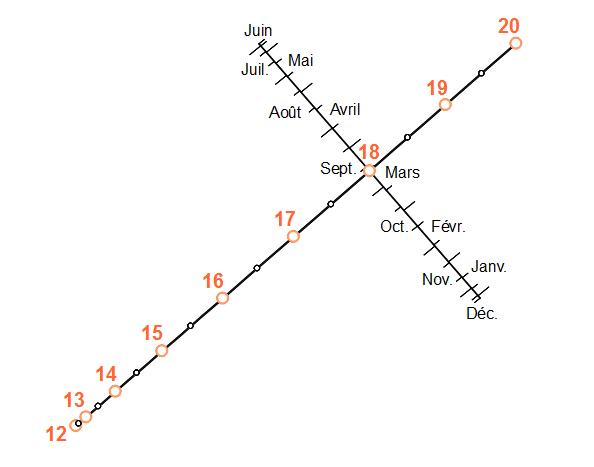
Bien que cela n’apparaisse pas de façon sensible, il faut noter que les droites des heures et des dates ne sont pas perpendiculaires. Elles le deviennent dans le cas du cadran de Parent ci-dessous où le plan est celui du méridien, soit une déclinaison correspondante de 90°.

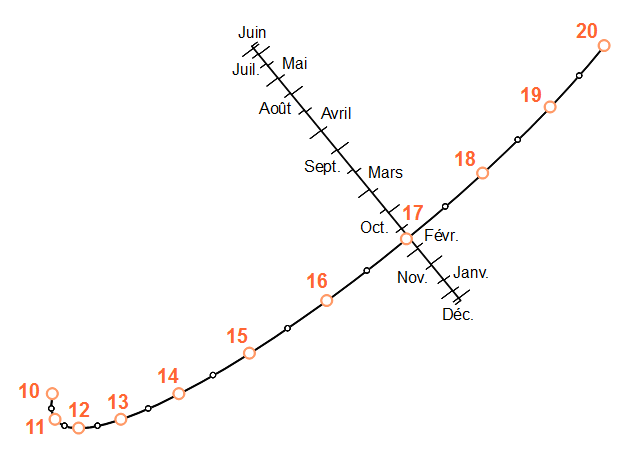
Bien sûr, j’aurais aussi pu choisir un style perpendiculaire au mur. Dans ce cas la droite horaire aurait pris la forme elliptique classique du cadran analemmatique comme on peut le voir ci-dessous.

Encore bravo Stéphane pour votre ténacité à chercher la solution.
Yvon Massé - Site perso. : La gnomonique
-
Stéphane_L
- Messages : 111
- Enregistré le : lun. 3 juin 2019 21:33
Re: Énigme gnomonique
Bon sang mais c’est bien sur !!
Il est évidemment plus simple de projeter la verge sur le plan du cadran.
Pour la déclinaison, c’est une erreur de calcul digne d’un élève de 6ème (90 – 29 ≠ 71) .
.
En ce qui concerne la proportion ligne de dates / droite horaire (de 12 h à 20 h dans le plan du méridien), elle est d’environ 3/5 avec une déclinaison de 61°(si ce n’est pas la bonne, je n’ai pas compris mon erreur).
En tout cas c’est un beau cadran, simple, pas trop difficile à réaliser (que du rectiligne, pas de courbes à tracer, et seulement deux segments). Reste toujours l'inclinaison précise du style qui reste pour moi un obstacle technique à ma première construction de cadran solaire.
Merci pour cette énigme qui m’a permis de progresser dans ce si grand domaine qu’est la gnomonique !
Il est évidemment plus simple de projeter la verge sur le plan du cadran.
Pour la déclinaison, c’est une erreur de calcul digne d’un élève de 6ème (90 – 29 ≠ 71)
En ce qui concerne la proportion ligne de dates / droite horaire (de 12 h à 20 h dans le plan du méridien), elle est d’environ 3/5 avec une déclinaison de 61°(si ce n’est pas la bonne, je n’ai pas compris mon erreur).
En tout cas c’est un beau cadran, simple, pas trop difficile à réaliser (que du rectiligne, pas de courbes à tracer, et seulement deux segments). Reste toujours l'inclinaison précise du style qui reste pour moi un obstacle technique à ma première construction de cadran solaire.
Merci pour cette énigme qui m’a permis de progresser dans ce si grand domaine qu’est la gnomonique !
- Yvon_M
- Administrateur du site
- Messages : 411
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Énigme gnomonique
À mon tour de faire mon mea culpa : j’ai mal interprété le dessin pour la proportion ligne de date / droite horaire. J’ai cru (pour quelle raison ?) que le point de 12 h était situé au point d’implantation de la verge et je ne retrouvais pas les cotes de 14,935 et 22,845. Après avoir estimé la bonne position du point de 12 h, j’obtiens bien à présent ces cotes et la proportions est donc correcte. Désolé d’avoir semé le trouble…
Il faut aussi signaler un autre défaut à ce cadran qui est effectivement sympathique à tracer : il ne peut pas indiquer l’heure aux périodes proches des solstices. Dans ce cas l’ombre du style se confond à la ligne horaire. Est-ce une des raisons pour laquelle le cadran de Parent soit resté confiné dans les comptes rendus de l’Académie des sciences ?
Il faut aussi signaler un autre défaut à ce cadran qui est effectivement sympathique à tracer : il ne peut pas indiquer l’heure aux périodes proches des solstices. Dans ce cas l’ombre du style se confond à la ligne horaire. Est-ce une des raisons pour laquelle le cadran de Parent soit resté confiné dans les comptes rendus de l’Académie des sciences ?
Yvon Massé - Site perso. : La gnomonique
- Yvon_M
- Administrateur du site
- Messages : 411
- Enregistré le : dim. 4 nov. 2018 01:54
- Localisation : Pontoise (Île-de-France)
- Contact :
Re: Énigme gnomonique
J’ai pensé qu’il pourrait être intéressant pour certain de savoir comment j’ai tracé les cadrans ci-dessus.
Comme vous le savez certainement, mon langage préféré pour faire ce genre de bricolage est Python. Je suis parti d’un script assez général qui dessine les cadrans analemmatiques sur toutes les orientations de plan à toutes les latitudes et suivant toutes les orientations du porte-ombre.
La difficulté n’est en soi pas si grande si on connaît bien le principe du cadran analemmatique, expliqué par exemple par R. Sagot dans cet article très pédagogique, et si on utilise les changements de repère évoqués sur ce fil.
Il « suffit » de définir le cadran armillaire dans le repère équatorial (c’est là où c’est le plus simple), de le ramener dans le repère du cadran et enfin de le projeter sur le cadran suivant la direction que devra prendre le porte-ombre.
Pour dessiner le cadran, je suis passé par un fichier dxf très simplifié dont j’ai rassemblé les routines pour le renseigner dans un script à part (fdxf.py). L’intérêt est que ce script peut ainsi être réutilisé pour d’autres applications.
L’avantage du fichier dxf est qu’il assez standard et il peut être relu avec différents logiciels libres dont LibreCAD ou LibreOffice. C’est ce dernier que j’ai utilisé pour modifier les caractéristiques des traits et rajouter les heures et les mois.
Voici donc les deux scripts qui sont assez court pour retrouverez facilement les principes énoncés plus haut :
Et le résultat brut que donne le fichier dxf dans LibreOffice Draw :
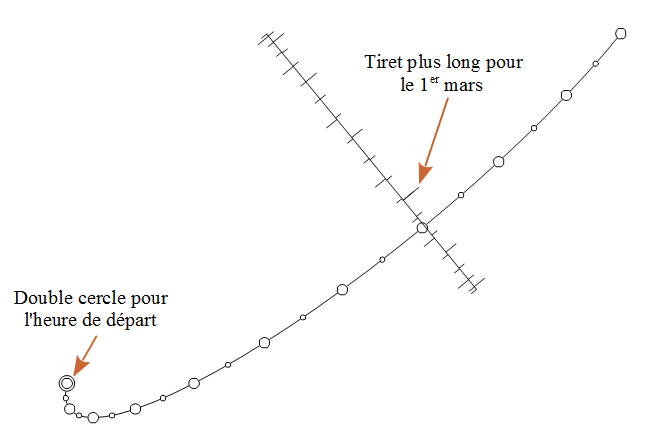
Comme vous le savez certainement, mon langage préféré pour faire ce genre de bricolage est Python. Je suis parti d’un script assez général qui dessine les cadrans analemmatiques sur toutes les orientations de plan à toutes les latitudes et suivant toutes les orientations du porte-ombre.
La difficulté n’est en soi pas si grande si on connaît bien le principe du cadran analemmatique, expliqué par exemple par R. Sagot dans cet article très pédagogique, et si on utilise les changements de repère évoqués sur ce fil.
Il « suffit » de définir le cadran armillaire dans le repère équatorial (c’est là où c’est le plus simple), de le ramener dans le repère du cadran et enfin de le projeter sur le cadran suivant la direction que devra prendre le porte-ombre.
Pour dessiner le cadran, je suis passé par un fichier dxf très simplifié dont j’ai rassemblé les routines pour le renseigner dans un script à part (fdxf.py). L’intérêt est que ce script peut ainsi être réutilisé pour d’autres applications.
L’avantage du fichier dxf est qu’il assez standard et il peut être relu avec différents logiciels libres dont LibreCAD ou LibreOffice. C’est ce dernier que j’ai utilisé pour modifier les caractéristiques des traits et rajouter les heures et les mois.
Voici donc les deux scripts qui sont assez court pour retrouverez facilement les principes énoncés plus haut :
Code : Tout sélectionner
def o_dxf(nfic): # Ouvrir le fichier dxf nfic
fic = open(nfic, 'w')
fic.write (' 0\nSECTION\n 2\nENTITIES\n')
return fic # Retourne son identifiant fic
def line(fic, pt1, pt2): # Tracer une ligne
fic.write(' 0\nLINE\n')
fic.write(' 10\n%1.3f\n 20\n%1.3f\n 30\n0.0\n' % pt1)
fic.write(' 11\n%1.3f\n 21\n%1.3f\n 31\n0.0\n' % pt2)
def polyline(fic, pts): # Tracer une polyligne
fic.write(' 0\nPOLYLINE\n 70\n8\n')
for pt in pts:
fic.write(' 0\nVERTEX\n 10\n%1.3f\n 20\n%1.3f\n 30\n0.0\n' % pt)
fic.write(' 0\nSEQEND\n')
def circle(fic, ct, ry): # Tracer un cercle
fic.write(' 0\nCIRCLE\n')
fic.write(' 10\n%1.3f\n 20\n%1.3f\n 30\n0.0\n' % ct)
fic.write(' 40\n%1.3f\n' % ry)
def c_dxf(fic): # Clore le fichier d'identifiant fic
fic.write(' 0\nENDSEC\n 0\nEOF\n')
fic.close()
Code : Tout sélectionner
from math import *
import fdxf
def Rot(x, y, r):
r *= pi/180
return cos(r)*x + sin(r)*y, -sin(r)*x + cos(r)*y
def EtoC(x, y, z): # Changement de coordonnées équatoriales --> cadran
z, x = Rot(z, x, 90 - phi) # ... dans le repère local
x, y = Rot(x, y, -D)
z, x = Rot(z, x, Z) # ... dans le repère cadran
return x, y, z
def Proj(x, y, z): # Projection sur le cadran avec mise à la dimension R
return R*(y - z*yp/zp), R*(z*xp/zp - x)
# Orientation du plan
phi = 49 # Latitude en °, négative dans l'hémisphère sud
D = 71 # Déclinaison en °, négative à l'est
Z = 90 # Inclinaison en ° ou distance zénithale
# Géométrie du tracé
R = 20.0 # Rayon du cadran en mm
prp = 50 # Rapport des longueurs de l'échelle des dates et des tirets
nsg = 3 # Nombre de segment par heure
rp = R/150 # Rayon des points
hd = 10 # Heure du premier point
hf = 20 # Heure du dernier point
# Constantes astronomiques pour le calcul de l'échelle des dates
k = .0172024
jm = 308.7
jl = 21.44
e = .0167
ob = .4091
# Direction de la projection dans le repère cadran
xp, yp, zp = 0, 0, 1 # projection orthogonale
# xp, yp, zp = EtoC(0, 1, 0) # direction de l'est
dxf = fdxf.o_dxf('cadran.dxf')
# Ligne horaire
pths = []
for hv in range(hd*nsg, hf*nsg + 1):
x, y = Rot(1, 0, 15.0*hv/nsg) # Direction du point horaire hv dans le repère polaire
pths.append(Proj(*EtoC(x, y, 0)))
fdxf.polyline(dxf, pths)
# Points des heures et des demi-heures
for hv in range(2*hd, 2*hf + 1):
x, y = Rot(1, 0, 15.0*hv/2) # Direction du point horaire hv dans le repère polaire
x, y = Proj(*EtoC(x, y, 0))
if hv == 2*hd: fdxf.circle(dxf, (x, y), 3*rp)
ct = 1
if hv % 2 == 0: ct = 2
fdxf.circle(dxf, (x, y), ct*rp)
# Ligne des dates
x1, y1 = Proj(*EtoC(0, 0, tan(-ob)))
x2, y2 = Proj(*EtoC(0, 0, tan(ob)))
dx, dy = (y2 - y1)/prp, (x1 - x2)/prp
fdxf.line(dxf, (x1, y1), (x2, y2))
# Tirets des dates
for mo in range(3, 15):
for jo in [1, 11, 21]:
# Nombre de jours écoulés depuis le 1 Mars O h TU
j = int(30.61*(mo + 1)) + jo - 122.5
# Anomalie et longitude moyenne
m = k*(j - jm)
l = k*(j - jl)
# Longitude vrai
s = l + 2*e*sin(m) + 1.25*e*e*sin(2*m)
z = sin(ob)*sin(s)
x, y = Proj(*EtoC(0, 0, z/sqrt(1 - z*z)))
ct = 1
if cos(s) < 0: ct = -1
if jo == 1:
if mo == 3:
fdxf.line(dxf, (x, y), (x + 3*ct*dx, y + 3*ct*dy))
ct *= 2
fdxf.line(dxf, (x, y), (x + ct*dx, y + ct*dy))
fdxf.c_dxf(dxf)

Yvon Massé - Site perso. : La gnomonique