Ozanam a proposé différents types de ces cadrans qu’il a classés suivant les courbes obtenues pour le réseau d’heure ou de latitude : linéaire, elliptique, hyperbolique et parabolique. Bien que ses ouvrages traitant de gnomonique, notamment ses célèbres Récréations mathématiques et physiques, aient été publiés de nombreuses fois jusqu’au milieu du XVIIIe siècle, ses cadrans universels n’ont été commentés qu’à une époque récente (2). Les auteurs qui se sont penchés sur l’analyse de leurs tracés ont utilisé la géométrie analytique. Elle a l’avantage de confirmer la validité des figures mais, à mon goût, elle n’a pas l’élégance et la pédagogie de la géométrie pure. Le but de ce sujet est donc de décrire ces cadrans universels d’une manière plus ludique et peut-être plus proche de la façon dont Ozanam les a imaginés.
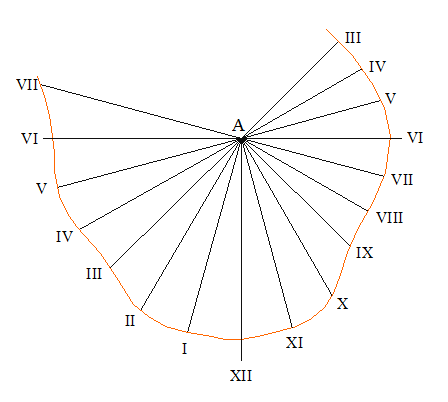
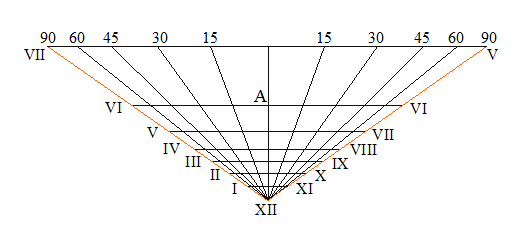
Ozanam introduit ses cadrans universels en proposant une adaptation à l’analemme de St Rigaud : une série de courbes en point-tillé qu’il superpose aux lignes horaires, il précise que ce sont des ellipses.
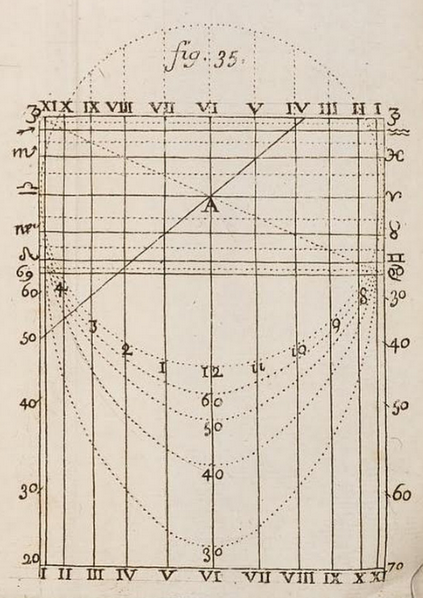
L’affectation des lignes horaires de l’analemme est redéfinie par une numérotation en chiffre arabe sur l’ellipse supérieure qui, ici, est plus exactement le cercle correspondant à la latitude de 90°. Les autres ellipses sont paramétrées avec la valeurs de la latitude. Les lignes horaires doivent être orientées suivant la méridienne, la partie basse de la figure en direction du nord. Le style doit être implanté au point A et incliné suivant le latitude du lieu.
On peut retrouver ces ellipses en imaginant une surface fictive cylindrique dont l’axe est le style polaire et le diamètre celui de la largeur de l’analemme (voir figure suivante). Sur cette surface les lignes horaires sont des droites espacées régulièrement. Situons-nous à une certaine latitude, l’ombre du style à une heure donnée court sur le plan horizontal pour aller recouvrir la ligne horaire correspondante du cylindre.
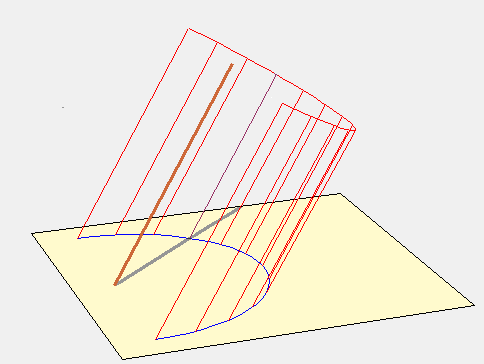
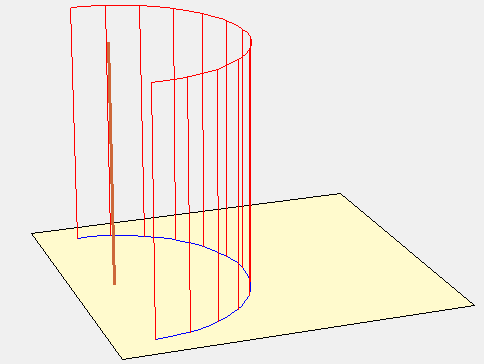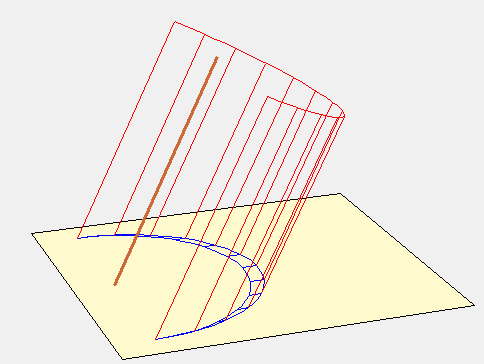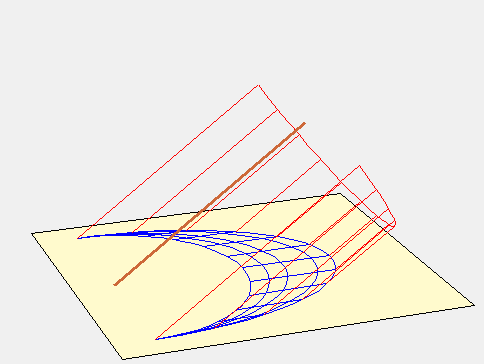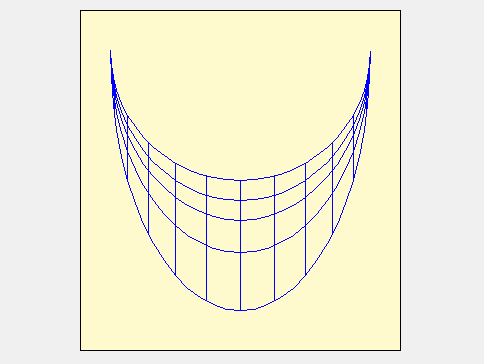
On peut donc considérer l’intersection de ce cylindre avec l’horizon comme la courbe de latitude du lieu où nous sommes situés en attribuant aux points horaires l’endroit où les lignes horaires fictives percent le plan de l’horizon. Ces points devront être reliés aux points horaires des autres latitudes pour obtenir les courbes horaires qui, dans ce cas, seront des droites parallèles. C’est ce qui est fait sur l’animation suivante où la latitude varie de 90° à 30° afin de retrouver la figure proposée par Ozanam.
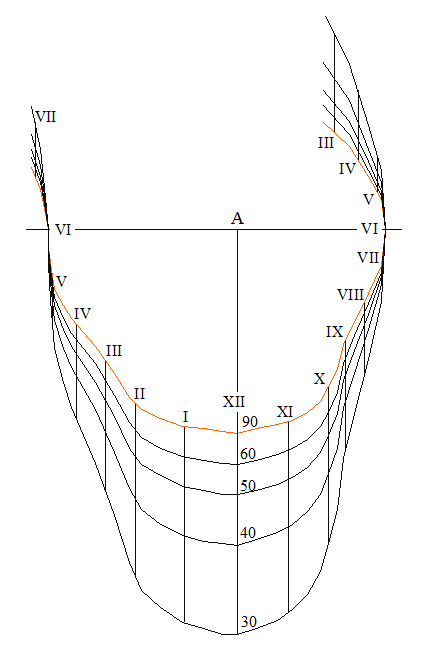
Ensuite Ozanam propose son cadran elliptique universel qui se présente ainsi :
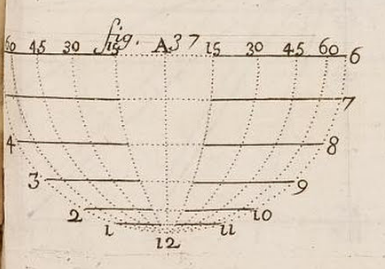
Le style doit être implanté en A et la ligne A-12 orientée suivant la méridienne, le 12 en direction du nord. Les lignes horaires sont des droites dirigées est-ouest et les courbes de latitude des ellipses qui s’aplatissent sur la méridienne quand la latitude diminue. Le paramétrage des ellipses est situé au dessus de la ligne des 6 heures.
On peut expliquer le tracé de ce cadran avec le même cylindre fictif que précédemment mais en faisant varier son diamètre en fonction de la latitude de telle sorte que sa ligne fictive de midi perce le plan horizontal toujours au même endroit.
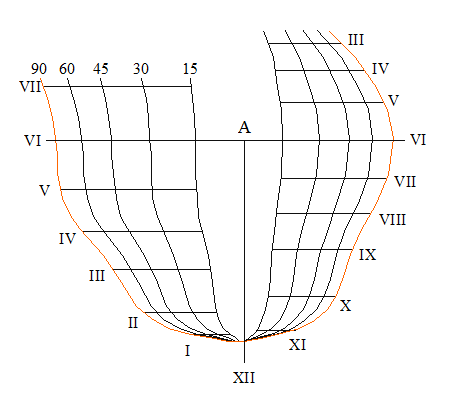
Ozanam présente ensuite 2 cadrans rectilignes universels. Le premier est uniquement constitué de lignes orthogonales. Je présenterai d’abord le second qui peut s’apparenter plus facilement au cadran de l’analemme de St Rigaud. Voici la figure correspondante :
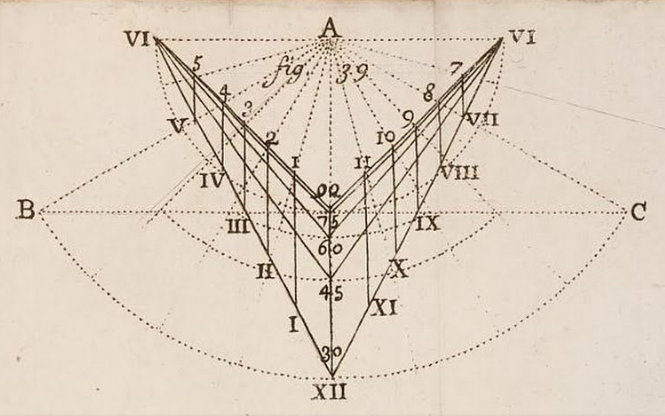
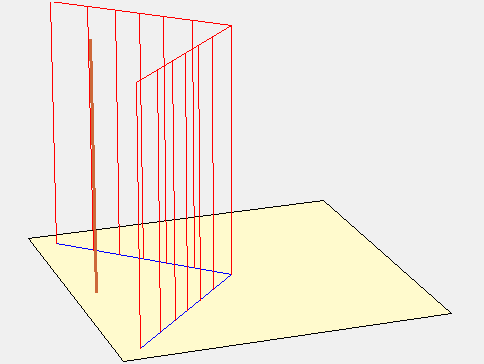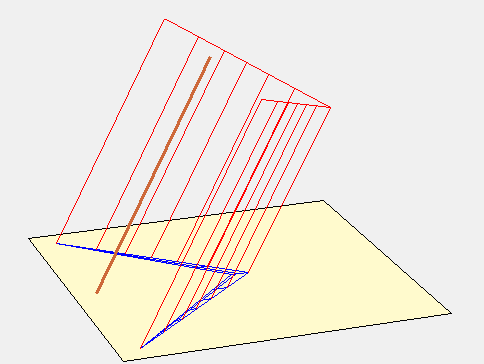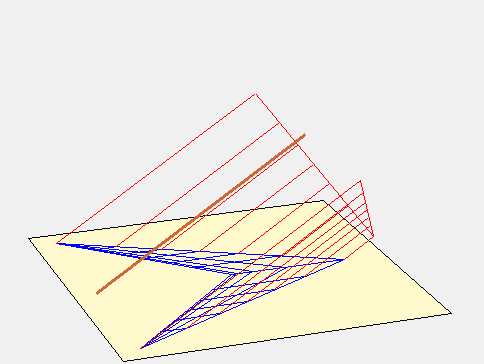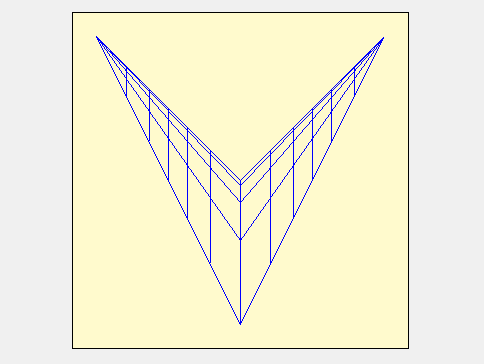
Les lignes horaires sont parallèles et doivent être disposées suivant la méridienne, le XII vers le nord. Le style doit être implanté en A et incliné suivant le latitude du lieu. Les courbes de latitude sont des droites brisées en forme de V.
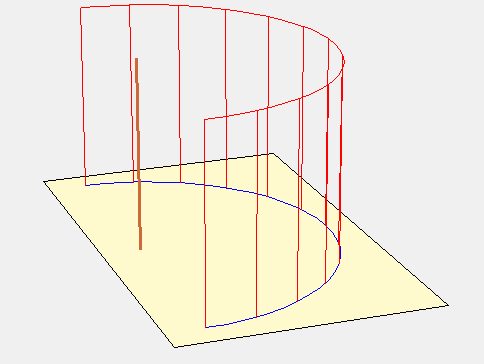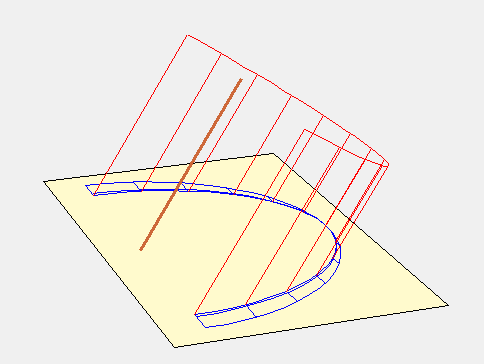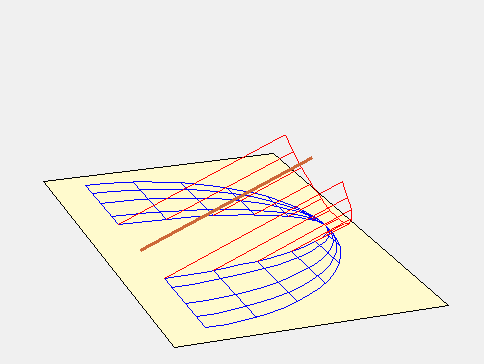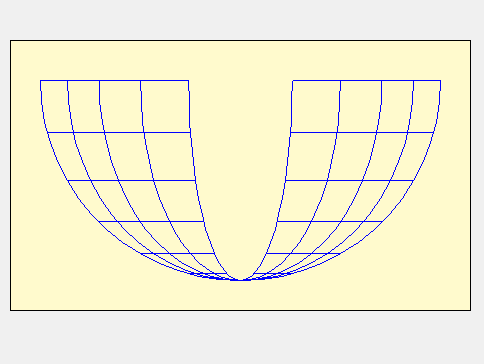
La surface fictive pour expliquer ce tracé est constituée de 2 portions de plan parallèles au style et qui se rejoignent au niveau de la ligne fictive de midi. L’animation suivante parle d’elle-même.
Le cadran à lignes orthogonales est un peu plus difficile à interpréter car c’est en fait la superposition de 2 cadrans différents. Le premier, qui est réparti sur toute la surface, a des lignes horaires est-ouest et des lignes de latitudes nord-sud. À l’inverse le second, qui ne s’étend que sur le tiers inférieur du cadran, a des lignes horaires nord-sud tandis que les lignes de latitude sont est-ouest.
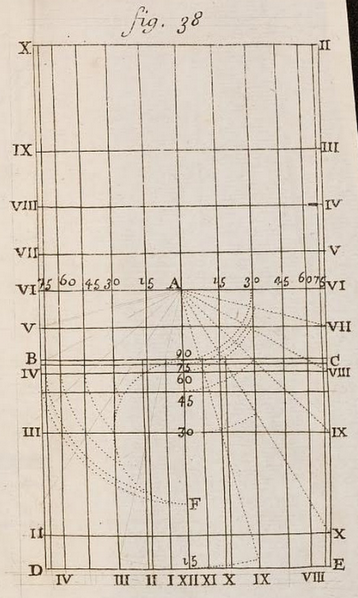
Les graduations horaires sont situées sur le pourtour du cadran, celles des latitudes le long des médianes. Comme pour tous les cadrans précédents, le XII est à placer vers le nord et le style doit être implanté en A.
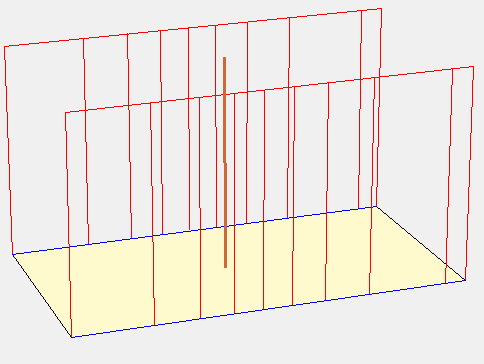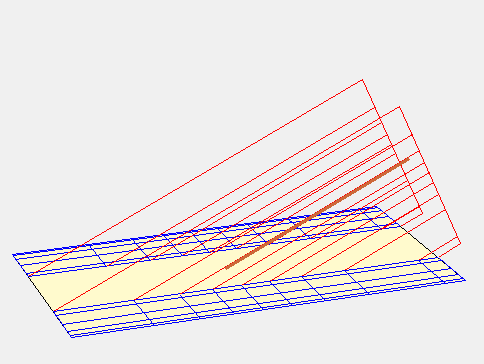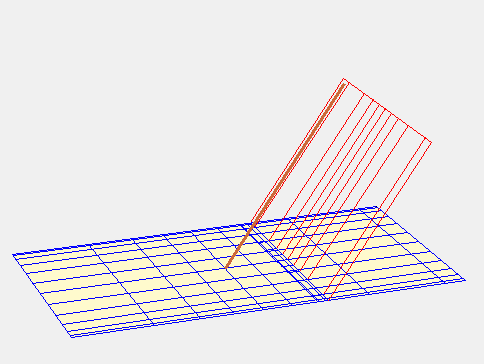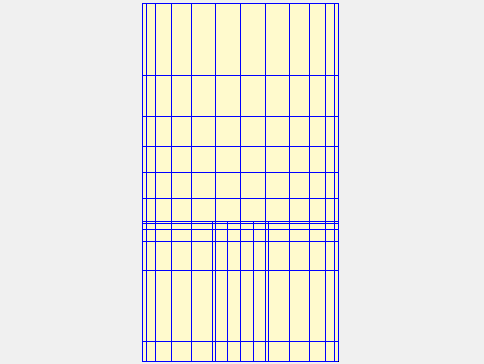
Les surfaces fictives qui sont à l’origine des lignes horaires est-ouest sont 2 portions de plan qui correspondent, pour le premier, à un cadran oriental et, pour le second, à un cadran occidental. Ces cadrans se rapprochent du style quand la latitude diminue. Quant aux autres lignes horaires, elles sont dues à une portion de plan qui donne un cadran polaire.
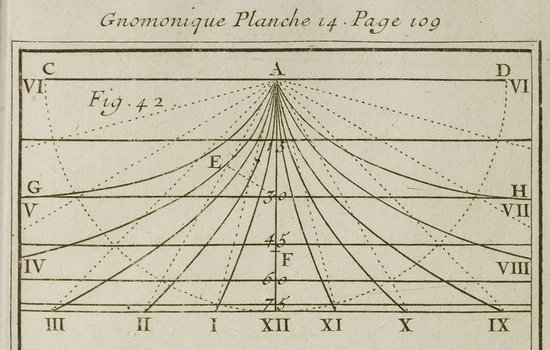
Ozanam nous propose ensuite un cadran universel hyperbolique. Cette fois ce sont les courbes horaires qui sont à l’origine de la dénomination tandis que les latitudes sont représentées par des lignes parallèles orientées est-ouest. Le point A où doit être implanté le style est situé à l’intersection des asymptotes et toutes les hyperboles passent par le point B situé sur la ligne de latitude 0°.
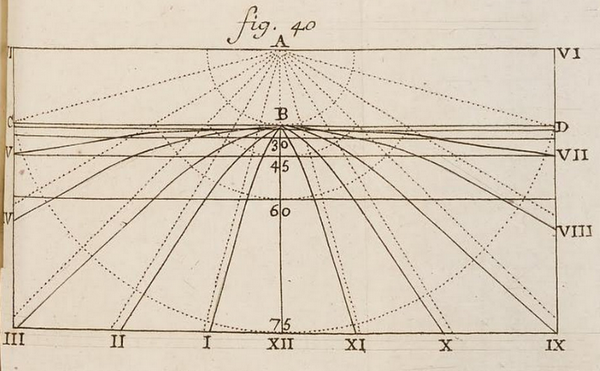
Cette fois-ci, la surface fictive correspond à celle d’un cadran équatorial.
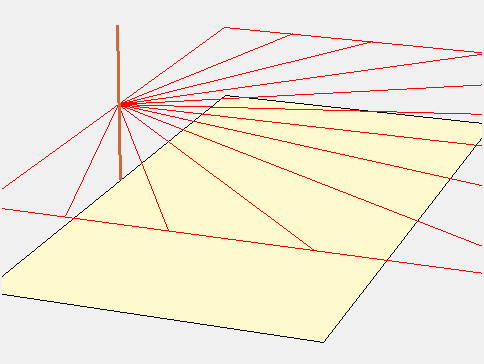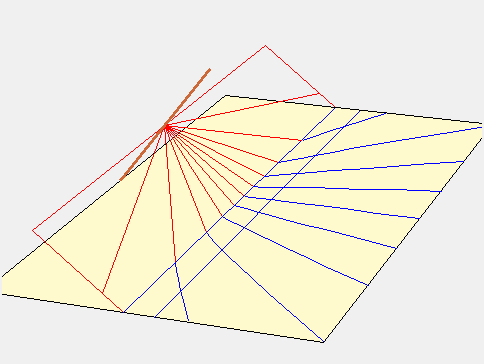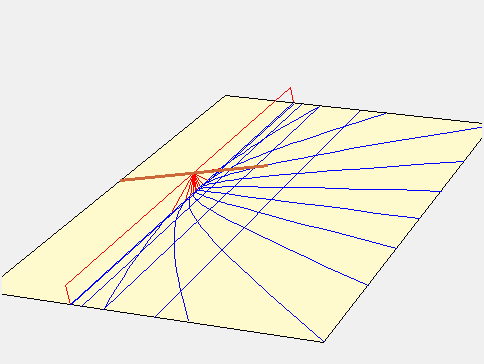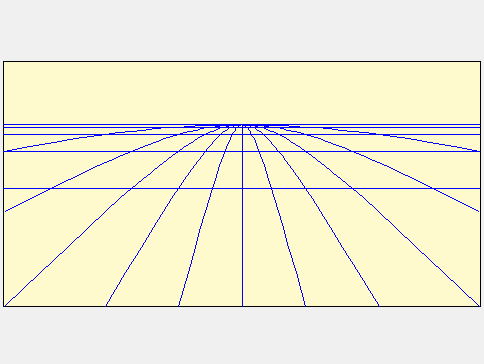
En changeant de latitude, le style entraîne dans son mouvement de rotation les lignes horaires fictives qui décrivent des hyperboloïdes comme on peut en voir un sur l’image suivante prélevée sur le site Wikipédia.

Le plan du cadran passe par l’axe de cette rotation, les courbe horaires correspondent donc à la génératrice (ou au « profil ») des hyperboloïdes, ce sont des hyperboles.
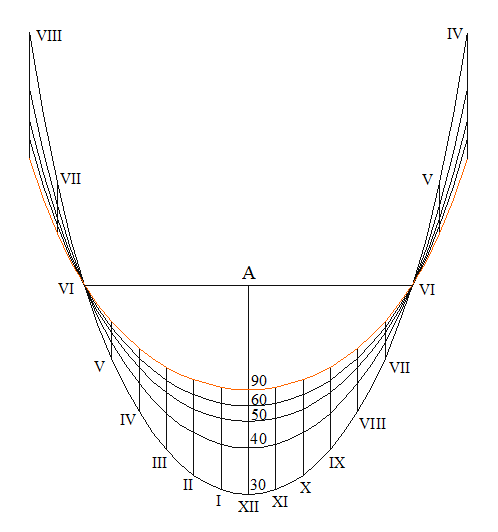
Le dernier cadran dit parabolique n’a pas été publié dans la première édition des Méthodes pour tracer des cadrans mais est apparu 8 ans plus tard dans les Cours de mathématiques. On peut penser qu’Ozanam a souhaité compléter la famille des coniques par un cadran qu’il n’a pas trouvé tout de suite. Je dois confier que de mon côté j’ai eu beaucoup plus de mal à trouver la surface fictive correspondante. Voici donc ce cadran ou l’on retrouve des lignes de latitudes parallèles et orientées est-ouest
La figure reprend tous les codes précédents : le point A pour l’implantation du style et la graduation des lignes de latitude en chiffre arabe le long de la ligne de midi. Quant à la surface fictive correspondante, elle est effectivement un peu plus spécifique, c’est un demi-cylindre dont le diamètre correspond à la hauteur du cadran.

J’espère que ce tour d’horizon des cadrans universels d’Ozanam vous a intéressé. Je vous proposerai un nouveau message avec 2 voies de généralisation de ces cadrans parmi l’infinité des tracés possibles.
1 ^ - Premières éditions des ouvrages d’Ozanam traitant entièrement ou en partie de gnomonique :
- Méthode générale pour tracer des cadrans sur toute sorte de plans (première édition 1685), pp. 132-144, planches
- Méthode générale pour tracer des cadrans sur toute sorte de plans (seconde édition 1697), pp. 143-156, planches dans le texte
- Cours de mathématique, tome 5 (première édition 1693), pp. 102-109, planches dans le texte
- Récréations mathématiques et physiques, tome 1 (première édition 1694), pp. 292-300, planches dans le texte
- DRECKER : Die Theorie der Sonnenuhren. Berlin, 1925
- De RIJK : Het pientere H-lat-netwerk van meneer Ozanam. Zonnewijzerkring bulletin XIV, p. 716. Sept. 1982
- ROHR : Die eigenartigen Sonnenuhren des Jaques Ozanam. Zonnewijzerkring 85.3, pp. 337-342. Sept. 1985
- De VRIES : Aanvullingen Ozanam-zonnewijzers. Zonnewijzerkring 85.4. Déc. 1985
- ROHR : Les cadrans solaires universels de Jacques Ozanam. Centaurus vol. 29-3, pp. 165-177. Sept. 1986
- SAWYER : Quiz Answer: Jacques’ Layout. The Compendium vol. 7 n° 2, pp. 18-22. Juin 2000