Cette méthode a aussi la particularité de pouvoir s’appliquer à la photo d’un cadran et ceci quelque soit l’angle de la prise de vue. Denis Savoie, qui a reporté la méthode de R. Sagot dans son livre Gnomonique moderne p. 196, démontre cette possibilité en affirmant simplement que « la photo d’une projection gnomonique est une projection gnomonique », sans donner aucun détail supplémentaire.
M’étant récemment plongé dans des problèmes de perspective, j’étais curieux de savoir comment on pouvait démontrer une telle affirmation ou, plus particulièrement, comment montrer que la méthode des tangentes s’appliquait toujours sur une photo prise en oblique. J’ai finalement obtenu la réponse et je vous propose de partager la démonstration.
Nous considérerons donc pour acquis que la méthode des tangentes s’applique au tracé du cadran, ce qui est longuement démontré dans l’article de R. Sagot et qu’on peut aussi montrer très facilement à partir des considérations proposées à la fin du message viewtopic.php?p=141#p141
Pour notre démonstration, nous devons faire la connaissance avec une quantité invariante en perspective qui est appelée birapport. Le birapport est un nombre qui correspond au rapport de 2 rapports de 2 dimensions algébriques. Il y a ainsi 4 dimensions au total qui sont définies par 4 points pris dans un ordre donné le long d’une même droite. On peut donc considérer dans un premier temps que le birapport est un nombre associé à 4 points aligné A, B, C et D et que nous désignerons par (A, B ; C, D)
(A, B ; C, D) \(=\frac{\overline{CA}/\overline{CB}}{\overline{DA}/\overline{DB}}=\frac{\overline{CA}}{\overline{CB}}\cdot\frac{\overline{DB}}{\overline{DA}}\)
Si on fait la perspective ou la projection centrale de centre O de ces 4 points, on obtient 4 nouveaux points A', B', C' et D'. Ces derniers points sont aussi alignés car ils sont dans le plan de la vue en perspective ou de la projection, ainsi qu’à l’intersection du plan contenant les points O, A, B, C et D. Plaçons nous, figure suivante, dans ce dernier plan et traçons les parallèles à OA qui passent par B et B'. La première coupe OC en M et OD en N ; la seconde coupe OC en M' et OD en N'.
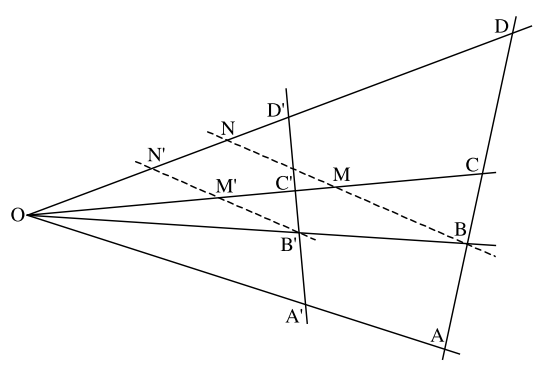
Appliquons le théorème de Thalès dans les triangles OAC et OAD, nous avons :
\(\frac{\overline{CA}}{\overline{CB}}=\frac{\overline{OA}}{\overline{MB}}\) et \(\frac{\overline{DA}}{\overline{DB}}=\frac{\overline{OA}}{\overline{NB}}\)
d’où : (A, B ; C, D) \(=\frac{\overline{CA}/\overline{CB}}{\overline{DA}/\overline{DB}}=\frac{\overline{NB}}{\overline{MB}}\)
On montrera de même avec les triangles OA'C' et OA'D' que :
(A', B' ; C', D') \(=\frac{\overline{C'A'}/\overline{C'B'}}{\overline{D'A'}/\overline{D'B'}}=\frac{\overline{N'B'}}{\overline{M'B'}}\)
En appliquant maintenant le théorème de Thalès aux triangles BMO et BNO nous obtenons :
\(\frac{\overline{OB}}{\overline{OB'}}=\frac{\overline{MB}}{\overline{M'B'}}\) et \(\frac{\overline{OB}}{\overline{OB'}}=\frac{\overline{NB}}{\overline{N'B'}}\) d’où : \(\frac{\overline{MB}}{\overline{M'B'}}=\frac{\overline{NB}}{\overline{N'B'}}\)
En croisant les extrêmes on obtient :
\(\frac{\overline{N'B'}}{\overline{M'B'}}=\frac{\overline{NB}}{\overline{MB}}\) d’où : (A', B' ; C', D') = (A, B ; C, D), ce qui signifie que la perspective conserve le birapport de 4 points alignés.
Indépendamment de cet aspect de perspective, considérons toujours la figure précédente mais dans le cas le plus général. Étant donné que toute droite qui coupe le faisceau de droites OA, OB, OC et OD donne 4 points d’intersection dont le birapport est constant, on peut aussi associer ce birapport au faisceau des 4 droites OA, OB, OC et OD. Notons aussi qu’à partir d’un point quelconque Q, qu’il soit dans le plan de la figure ou en dehors, le faisceau de droite QA, QB, QC et QD aura toujours le même birapport. Remarquons enfin qu’il est possible de simplifier le calcul du birapport d’un faisceau en choisissant une droite sécante parallèle à une des droites du faisceau comme la droite OA. Le 4ième point d’intersection est rejeté à l’infini et le birapport se simplifie pour donner un rapport simple comme \(\frac{\overline{NB}}{\overline{MB}}\) ou \(\frac{\overline{N'B'}}{\overline{M'B'}}\), ce que nous avons effectivement obtenu plus haut.
Ainsi, à tout faisceau de 4 droites comme par exemple 4 lignes d’heure d’un cadran, on peut associer un birapport qui restera constant en perspective. C’est à dire que dans notre exemple le birapport du faisceau des 4 lignes d’heure sur la photo du cadran sera le même que celui mesuré sur le cadran lui-même.
Considérons donc à présent le faisceau des 4 lignes horaires H-6, H, H+1 et H+2. Pour évaluer son birapport, plaçons une règle parallèlement à la ligne H-6, c’est à dire dans la position de la règle des tangentes. Aussi, conformément d’une part à ce que nous avons vu plus haut et d’autre part à ce qu’a montré R. Sagot, nous obtiendrons la valeur de \(\frac{\tan30°}{\tan15°}\), que ce soit sur le cadran ou sur la photo. Il suffit de refaire l’exercice avec tous les faisceaux obtenus en replaçant la ligne H+2 par les autres lignes du cadran qui rencontrent la règle maintenue au même endroit, pour se convaincre que le test des tangentes s’applique aussi bien sur le cadran lui-même que sur sa photo, quelque soit l’angle de la prise de vue.
Sur la photo suivante particulièrement déformée par la perspective, on peut constater que sur la ligne parallèle à celle de 4h, on retrouve une répartition en \(R\cdot\tan(n\cdot15°)\) de l’intersection des lignes horaires autours de l’intersection de la ligne de 10h.

